|
Question 637406: Good day tutors, I need your help with this function
How do I calculate the slope of
f(x) = -3x² + 5x
at the point P(-1,-8) ?
Found 2 solutions by ewatrrr, Edwin McCravy:
Answer by ewatrrr(24785)   (Show Source):
You can put this solution on YOUR website!
Hi,
f(x)= -3x^2 + 5x
f '(x) = -6x + 5, when x = -1 ⇒ f '(-1) =
y = mx + b (representing the Line tangent to the curve at x = -1)
y = 11x + b |Using Pt(-1,-8) to solve for b
-8 = 11 + b
3 = b
y = 11x + 3 is the line tangent ro the cureve at (-1,-8)
Answer by Edwin McCravy(20056)  (Show Source):
You can put this solution on YOUR website! Good day tutors, I need your help with this function
How do I calculate the slope of the tangent line to
f(x) = -3x² + 5x
at the point P(-1,-8) ?
What you are looking for is the slope of the black line which is tangent
to the parabola at the point (-1,-8)
Three ways to do it: (1) if you are beginning calculus and have not studied the
power rule, (2), if you are in calculus and have studied the power rule, and
(3) if you are in algebra or pre-calculus and haven't studied any calculus.
(1) If you are in calculus but haven't studied the power rule:
f'(x) =  =  =  =
 =  =  =
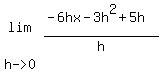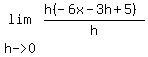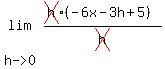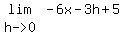 =  =  =  = -6x-3(0)+5 = -6x+5
f'(x) = -6x+5
f'(1) = -6(-1)+5 = 6+5 = 11
(2) If you've already studied the power rule 
then you can get
f'(x) = -6x+5 immediately from the power rule, as the lady above did.
f'(1) = -6(-1)+5 = 6+5 = 11
-------------------------------------------
(3) If you are studying algebra and haven't studed any calculus:
Suppose the line tangent to the graph of f(x) has the equation
y = mx + b
Write y for f(x)
y = -3x² + 5x
y = mx + b
Substitute the point (-1,-8) for (x,y) in y = mx+b:
-8 = m(-1) + b
-8 = -m + b
m - 8 = b
Substitute m - 8 for b
y = mx + m-8
Substitute for y in
y = -3x² + 5x
mx + m-8 = -3x² + 5x
3x² + mx - 5x + m-8 = 0
3x² + (m-5)x + m-8 = 0
A line is tangent to a parabola when the solution is a root
of multiblicity 2. This happens when the discriminant
B²-4AC = 0,
A=3, B =(m-5), C = m-8
Discriminant = B² - 4AC = (m-5)² - 4(3)(m-8) = m²-10m+25-12m+96 = m²+22m-121
So we set
m²+22m-121 = 0
(m-11)(m-11) = 0
m = 11
Edwin
|
|
|
| |
