Question 633882: The domain of the function f is {x: -1 < x < 5}. If g(x) = 2f(-x), what is the domain of the function g?
i know that the answer is (-5 < x < 1) but I am curious about the steps necessary to get that answer
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! For x such that 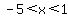 , then , then 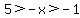 , which is the same as , which is the same as 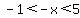 , so (-x) is in the domain of f(x). , so (-x) is in the domain of f(x).
Therefore, f(-x) is defined, and can be calculated and multiplied times 2 to find g(x).
For example,  exists, and so does exists, and so does  . .
On the other hand, when  , then , then  ,and ,and
(-x) is out of the domain of f(x).
For  , ,  is outside the domain of f(x). is outside the domain of f(x).
In either case case f(-x) does not exist, and neither does g(x).
For example for x=-5,  does not exist. It is not defined. does not exist. It is not defined.
The same goes for x=1. In that case,  does not exist either. does not exist either.
The function f(x) could be simply defined as f(x)=8 for x such that -1
If you like a fancier function, an example could be

|
|
|