|
Question 534799: Identify all Maximums Points, Minimum Points, and Points of Inflections for the function (x+3)/(x^2-16).
-----------------------------
I am not sure. I am thinking that ff there is no point at which the first derivative is equal to 0, then it is impossible for there to be a point at which both the second and first derivative are equal to 0, making the answer for all three points (Maximum, Minimum, and Points of Inflection) none.
My domain is all values of x except x=-2 & x=2. My range is (-infinity, infinity).
Thank you! :)
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! If it's really 
the points where it does not exist are x=-4 and x=4, and all other x are in the domain.
I agree that the range is (-infinity, infinity).
If that's really the function, it changes sign 3 times (at -4, -3 an 3), with vertical asymptotes at  and and 
and a zero at  . .
There is no minimum or maximum. The first derivative is always negative, so the function decreases continuously in each of the 3 regions where it exists, going from positive infinity at the right of vertical asymptote 
down to negative infinity on the left of vertical asymptote  . .
To hug those vertical asymptotes like that, the function has to go from concave upwards to concave downwards. The second derivative must have an inflection point somewhere between them. I calculated it, but I may have made a mistake. I got 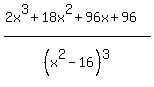
which is zero at a point near 
You do not need both derivatives to be zero to have an inflection point.
If they are both zero, it is a saddle point, an inflection point where the slope is zero. An example of a function with an inflection point where the first derivative is not zero is 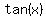 at at 
|
|
|
| |