|
Question 485840: the distance between the points (x,8) and (3,4) is 5 units. Then x is
Found 2 solutions by Jstrasner, MathTherapy:
Answer by Jstrasner(112)   (Show Source):
You can put this solution on YOUR website! Hey,
So for this problem we need to use the pythagorean theorem to discover what x is.
First, we need to plot the triangle that the two points are making:
First, the 8 and the 4 are the y measurements of the triangle, so if you subtract 4 from 8 you get 4. So we know that the measurement of the y leg is 4.
Second, the pythagorean theorem says that z^2 = x^2 + y^2
We know what the z and the y are: z=5 and y=4. So if we plug them into the equation we get:
5^2 = x^2 + 4^2 => 25 = x^2 + 16 => 9 = x^2 => x = 3
So if the x measurement is 3 then the x coordinate in the point must be 3 units away from (3,4) along the x axis. So the x coordinate is 3 + 3 = 6
Therefore, x = 6
It may be a little confusing but just plot out the triangle and use the pythagorean theorem, where the two short legs of the right triangle are the x and y and the long side, or the hypotenuse, is the z.
I hope this helps!
Answer by MathTherapy(10552)  (Show Source):
You can put this solution on YOUR website! the distance between the points (x,8) and (3,4) is 5 units. Then x is
Distance between these 2 points is 5 units
Using distance formula:  , and with D = 5,  ,  ,  , and  , we get:
 ------  ---- 
 ------- Squaring both sides of equation
 ------- 
x(x – 6) = 0
x = 0, or x – 6 = 0
x = 0, or x = 6
Therefore, x =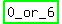 
--------
Check
--------
I believe you can do this!! If not, just use 0 in place of x in the ordered pair, then plug in each value into the distance formula to see if the distance is 5 units, as given.
Then use 6 in place of x in the ordered pair, plug in each value into the distance formula to see if the distance is 5 units, as given.
Send comments and “thank-yous” to MathMadEzy@aol.com
|
|
|
| |
