|
Question 361916: can you please explain the steps
state the domain of f(x)=9-18x
thank you
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! your equation is f(x) = 9 - 18*x
your range is the set of values that f(x) can take
your domain is the set of values that x can take.
in this equation, x can be anything, so the domain is the set of all real numbers.
the two main reasons the domain would be restricted are:
square root of a negative number.
division by 0.
neither one give you a real number as an answer so the values of x that result in an equation with a negative square root or with a division of 0 would be excluded from the domain.
in your equation, none of that is happening.
x can be negative.
x can be positive.
x can be 0.
the domain is all real number of x.
an example of an equation where the domain cannot be the set of all real numbers would be:
f(x) = 1/x
the domain is all real number except x = 0 since when x is equal to 0, the result is undefined because division by 0 is infinity and infinity is not a real number.
another example:
f(x) = square root of x.
x cannot be negative so the domain is all real numbers that are not negative.
the graph of your equation of f(x) = 9 - 18*x is shown below:

it's a straight line where y gets more positive as x gets more negative, and y gets more negative as x gets more positive.
there is no discontinuity where the value of y can't be plotted.
the graph of the equation of y = 1/x is shown below:
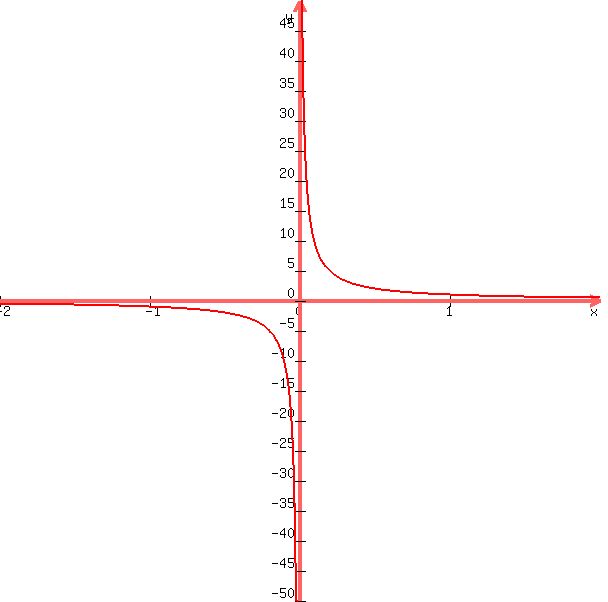
you can see the discontinuity around x = 0.
as x approaches 0 from the negative side, the value of y tends towards infinity in a negative direction.
as x approaches 0 from the positive side, the value of y tends towards infinity in a positive direction.
the graph of y = square root of x is shown below:
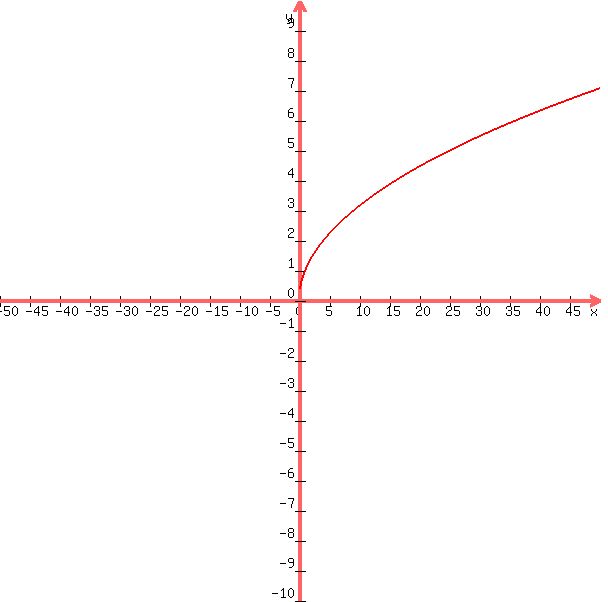
you can see that the value of x are positive or 0 only.
once again, the domain is the set of values that x can take and the range is the set of values that f(x) can take.
the range is dependent on the equation that ties the value of f(x) to x.
in the first graph, the range is the set of all real numbers.
in the second graph, the range is the set of all real numbers except 0.
f(x) cannot be 0 because 1 / x will never be 0 no matter how large x gets.
it will be very small but never 0.
in the third graph, the range is the set of all real numbers greater than or equal to 0.
there's a wrinkle here that you probably need to be aware of.
if i give you an equation that says that y = square root of x, then you would take the positive square root of x only.
if i give you an equation that says that y^2 = x, and you are solving for y, then your answer would be +/- square root of x.
the difference is in what you are given.
the first equations states that you are to take only the positive square root of x.
the second equation states that you are to solve for y. the solution is both positive square root of x and negative square root of x.
an example:
y^ = 25
y = +/- 5 because 5^2 = 25, and (-5)^2 = 25.
|
|
|
| |