|
Question 246034: consider the functions f(x)=-x^2+3x+10 and g(x)=2x^2+2x+11/4. what is the exact distance between the vertices of the graphs of these two functions? cannot use graphing to answer.
hopefully this will be my last question of the year.
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! Part 1) Find the vertices of  and and 
part a) Let's find the vertex of 
In order to find the vertex, we first need to find the x-coordinate of the vertex.
To find the x-coordinate of the vertex, use this formula:  . .
 Start with the given formula. Start with the given formula.
From  , we can see that , we can see that  , ,  , and , and  . .
 Plug in Plug in  and and  . .
 Multiply 2 and Multiply 2 and  to get to get  . .
 Reduce. Reduce.
So the x-coordinate of the vertex is  . Note: this means that the axis of symmetry is also . Note: this means that the axis of symmetry is also  . .
Now that we know the x-coordinate of the vertex, we can use it to find the y-coordinate of the vertex.
 Start with the given equation. Start with the given equation.
 Plug in Plug in  . .
 Square Square  to get to get  . .
 Multiply Multiply  and and  to get to get 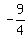 . .
 Multiply Multiply  and and  to get to get  . .
 Combine like terms. Combine like terms.
So the y-coordinate of the vertex is  . .
So the vertex is ) . .
------------------------
b) Now let's find the vertex of 
In order to find the vertex, we first need to find the x-coordinate of the vertex.
To find the x-coordinate of the vertex, use this formula:  . .
 Start with the given formula. Start with the given formula.
From  , we can see that , we can see that  , ,  , and , and  . .
 Plug in Plug in  and and  . .
 Multiply 2 and Multiply 2 and  to get to get  . .
 Reduce. Reduce.
So the x-coordinate of the vertex is  . Note: this means that the axis of symmetry is also . Note: this means that the axis of symmetry is also  . .
Now that we know the x-coordinate of the vertex, we can use it to find the y-coordinate of the vertex.
 Start with the given equation. Start with the given equation.
 Plug in Plug in  . .
 Square Square  to get to get  . .
 Multiply Multiply  and and  to get to get  . .
 Multiply Multiply  and and  to get to get  . .
 Combine like terms. Combine like terms.
So the y-coordinate of the vertex is  . .
So the vertex is ) . .
--------------------------------------------------
So to recap, the vertices of  and and  are are ) and and ) respectively. respectively.
===============================================================
Part 2) Now use the distance formula to find the distance between the two vertices (which are essentially points)
Note: ) is the first point is the first point ) . So this means that . So this means that  and and  . .
Also, ) is the second point is the second point ) . So this means that . So this means that  and and  . .
 Start with the distance formula. Start with the distance formula.
 Plug in Plug in  , ,  , ,  , and , and  . .
 Subtract Subtract  from from  to get to get  . .
 Subtract Subtract  from from 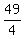 to get to get  . .
 Square Square  to get to get  . .
 Square Square  to get to get  . .
 Add Add  to to  to get to get 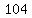 . .
 Simplify the square root. Simplify the square root.
So our answer is 
So the exact distance between the two vertices is 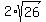 units. units.
|
|
|
| |