|
Question 215676: 1- Give the new coordinates if the point (4,-6) is transformed in the following manner: reflected across the y-axis, vertically compressed by a factor of one-half, and translated 6 units to the right. Show work.
2- A rectangle is enclosed by the x-axis and the graph of y= 3-|1/2 x|, with two vertices on the x-axis and two vertices on the given function. What are the dimensions of the rectangle that will yield the maximum area?
3- Suppose f is a function such that for all real number x. f(x-4) = x^2-2x. Find f(x)
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! Give the new coordinates if the point (4,-6) is transformed in the following manner: reflected across the y-axis: (4,6)
---------------------------------------------------
vertically compressed by a factor of one-half: (4,3)
---------------------------------------------------
and translated 6 units to the right: (10,3)
---------------------------------------------------
2- A rectangle is enclosed by the x-axis and the graph of y= 3-|1/2 x|, with two vertices on the x-axis and two vertices on the given function. What are the dimensions of the rectangle that will yield the maximum area?
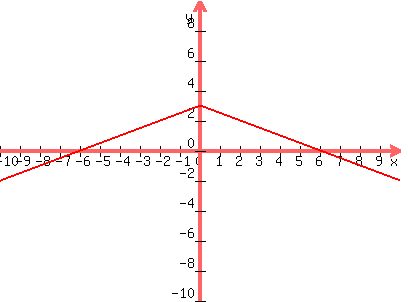
------
Let the base vertices be (-x,0) and (x,0).
The base width = 2x
--------
altitude = 3 -(1/2)x
---------------------------
Area = 2x(3-(1/2)x) = -x^2+6x
Maximum occurs when x = -b/2a = -6/(-2) = 3
------------------------------------------------
A(3) = -(3)^2 + 6*3 = 9 (That is the maximum area)
======================================================
3- Suppose f is a function such that for all real number x. f(x-4) = x^2-2x. Find f(x)
---
Since f(x) had moved 4 to the right when it became f(x-4)
replace x by (x+4) to find f(x).
f(x) = (x+4)^2-2(x+4) = x^2+8x+16-2x-8 = x^2+6x+8
=====================================================
Cheers,
Stan H.
|
|
|
| |