|
Question 185101This question is from textbook college algebra concepts and models
: find all real zeros of the function algebraically ie  . .
analyze the graph of the function algebraically ie  .
This question is from textbook college algebra concepts and models .
This question is from textbook college algebra concepts and models
Answer by ZeratuelX(5)   (Show Source): (Show Source):
You can put this solution on YOUR website! Finding all real zeros means that we are finding all possible values for x that will satisfy the equation and still are in the "real number system".
If we have the function  we are looking for all of the x-intercepts, which are the same as roots/zeros. The best way to find these algebraically is to factor it out. In this function there is an x we can factor out from the beginning. we are looking for all of the x-intercepts, which are the same as roots/zeros. The best way to find these algebraically is to factor it out. In this function there is an x we can factor out from the beginning.

Now we are looking for 2 numbers that add up to be 1, and multiply to be -6. The two numbers I came up with are -2 and 3. Let's factor this out using the reverse FOIL method and these numbers.

Since we are finding the zeros, which are essentially roots/x-intercepts, we can set y = 0 because the x-intercept will have a y coordinate of 0. We now have this equation:

Now by the zero factor theorem, if the product is 0, than we can set each factor to 0.



Now we solve for x in each of these.
 Solved. Solved.
-----


 2 Answers. 2 Answers.
 Solved. Solved.
-----


 2 Answers. 2 Answers.
 Solved. Solved.
The first equation is already solved, we already have 1 real root. The second equation can't be done in the real number system since we cannot take the square root of a negative number without using the imaginary number system. The third equation has two possible values, both of which are real and satisfy the equation.
-----
In the original equation we had 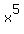 . Since it is raised to the 5th power, there are 5 total solutions, and we have found 3 of them to be real zeroes. The other two are imaginary numbers (from case 2). So our answer would be: . Since it is raised to the 5th power, there are 5 total solutions, and we have found 3 of them to be real zeroes. The other two are imaginary numbers (from case 2). So our answer would be:

 Note that these numbers are irrational, but still real. Note that these numbers are irrational, but still real.
 This is because they represent a decimal, that is between two numbers. This is because they represent a decimal, that is between two numbers.
===============
For your second question, we need to graph it and describe the graph. So the equation would look like this:


We can see that the graph opens down. Since it is a parabola, it starts going up, but it hits a vertex at (5,9) and then starts to go down.
|
|
|
| |