|
Question 162851This question is from textbook Precalculus with Limits a Graphing Approach Third Edition
: I need an explanation on how to solve this problem:
Determine the domain of the function
f(x)
Thank you
This question is from textbook Precalculus with Limits a Graphing Approach Third Edition
Answer by Earlsdon(6294)   (Show Source):
You can put this solution on YOUR website! Determine the domain:
Recall that the domain of a function is the set of all of the values of the independent for which the function is defined, in other words, all of the x-coordinate values.
 Notice that, for some values of x, the radicand becomes negative and, at these points, the function is not defined, thus these values of x would be excluded values.
What values of x would make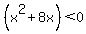 
The answer might be easier to see if you were to factor the radicand:
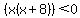
If x = -7, you would have:
 So x = -7 is a candidate for eclusion.
if x = -6, you would have:
 So x = -6 is a candidate for exclusion.
.
.
.
If x = -1, you would have:
 So x = -1 is a candidate for exclusion.
For all other values of x, the function is defined.
So the domain would be:
|
|
|
| |
