SOLUTION: For the function y = 3x^2 + 12x + 9 find: A. Whether the curve is concave up or down B. The y-intercept C. The x-intercept D. The Vertex E. The Maximum or Minimum

Algebra ->  Functions -> SOLUTION: For the function y = 3x^2 + 12x + 9 find: A. Whether the curve is concave up or down B. The y-intercept C. The x-intercept D. The Vertex E. The Maximum or Minimum       Log On


   

Question 154223: For the function y = 3x^2 + 12x + 9 find:
A. Whether the curve is concave up or down
B. The y-intercept
C. The x-intercept
D. The Vertex
E. The Maximum or Minimum value.
Answer by jim_thompson5910(35256) About Me  (Show Source):
You can put this solution on YOUR website!
y = 3x^2 + 12x + 9 ... Start with the given equation.


y' = 6x + 12 ... Find the first derivative


y'' = 6 ... Find the second derivative


Since y'' is always positive, this means that the function is concave up.


-------------

b)

Y-Intercept:

y=3x%5E2+%2B+12x+%2B+9 Start with the given equation.


y=3%280%29%5E2+%2B+12%280%29+%2B+9 Plug in x=0.


y=3%280%29%2B12%280%29%2B9 Square 0 to get 0.


y=0%2B12%280%29%2B9 Multiply 3 and 0 to get 0.


y=0%2B0%2B9 Multiply 12 and 0 to get 0.


y=9 Combine like terms.


So the y-intercept is (0,9)


----------------------

c)

X-Intercept(s):


y=3x%5E2+%2B+12x+%2B+9 Start with the given equation.


0=3x%5E2+%2B+12x+%2B+9 Plug in y=0


Notice we have a quadratic equation in the form of ax%5E2%2Bbx%2Bc where a=3, b=12, and c=9


Let's use the quadratic formula to solve for x


x+=+%28-b+%2B-+sqrt%28+b%5E2-4ac+%29%29%2F%282a%29 Start with the quadratic formula


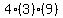x+=+%28-%2812%29+%2B-+sqrt%28+%2812%29%5E2-4%283%29%289%29+%29%29%2F%282%283%29%29 Plug in a=3, b=12, and c=9


x+=+%28-12+%2B-+sqrt%28+144-4%283%29%289%29+%29%29%2F%282%283%29%29 Square 12 to get 144.


x+=+%28-12+%2B-+sqrt%28+144-108+%29%29%2F%282%283%29%29 Multiply 4%283%29%289%29 to get 108


x+=+%28-12+%2B-+sqrt%28+36+%29%29%2F%282%283%29%29 Subtract 108 from 144 to get 36


x+=+%28-12+%2B-+sqrt%28+36+%29%29%2F%286%29 Multiply 2 and 3 to get 6.


x+=+%28-12+%2B-+6%29%2F%286%29 Take the square root of 36 to get 6.


x+=+%28-12+%2B+6%29%2F%286%29 or x+=+%28-12+-+6%29%2F%286%29 Break up the expression.


x+=+%28-6%29%2F%286%29 or x+=++%28-18%29%2F%286%29 Combine like terms.


x+=+-1 or x+=+-3 Simplify.


So the answers are x+=+-1 or x+=+-3


So the x-intercepts are (-1,0) and (-3,0)


----------------------------

d)

Vertex:


In order to find the vertex, we first need to find the x-coordinate of the vertex.


To find the x-coordinate of the vertex, use this formula: x=%28-b%29%2F%282a%29.


x=%28-b%29%2F%282a%29 Start with the given formula.


From y=3x%5E2%2B12x%2B9, we can see that a=3, b=12, and c=9.


x=%28-%2812%29%29%2F%282%283%29%29 Plug in a=3 and b=12.


x=%28-12%29%2F%286%29 Multiply 2 and 3 to get 6.


x=-2 Divide.


So the x-coordinate of the vertex is x=-2. Note: this means that the axis of symmetry is also x=-2.


Now that we know the x-coordinate of the vertex, we can use it to find the y-coordinate of the vertex.


y=3x%5E2%2B12x%2B9 Start with the given equation.


y=3%28-2%29%5E2%2B12%28-2%29%2B9 Plug in x=-2.


y=3%284%29%2B12%28-2%29%2B9 Square -2 to get 4.


y=12%2B12%28-2%29%2B9 Multiply 3 and 4 to get 12.


y=12-24%2B9 Multiply 12 and -2 to get -24.


y=-3 Combine like terms.


So the y-coordinate of the vertex is y=-3.


So the vertex is .


----------------------------

e)

Maximum or Minimum value:


Since the function is concave up, this means that the function has a minimum. The max/min value correspond to the y coordinate of the vertex. So the minimum value is y=-3


-----------------------------

Here's a graph to verify our answers:


+graph%28+500%2C+500%2C+-10%2C+10%2C+-10%2C+10%2C+3x%5E2%2B12x%2B9%29+ Graph of y=3x%5E2%2B12x%2B9