SOLUTION: I need to state the domain of the following. A) {{{g(x)=5x/(x^2+25)}}} B) {{{f(x)=sqrt(x+6)}}} C) {{{k(t)=5t^2-6t+2}}} D) {{{k(x)=(3x+3)/(x+2)}}} E) {{{m(x)=5x-7}

The domain is the set of all real numbers which can be
substituted for x and there will be a real value of the 
function. 

1. If there are no roots with an even index, or denominators 
containing the variables then the domain is always (, ). 
This domain graphed on a number line is:

<========================================================>
 -9 -8 -7 -6 -5 -4 -3 -2 -1  0  1  2  3  4  5  6  7  8  9 

In other words, the whole number line is shaded.  It is the
same as saying "any real number may be substituted for x and
a defined real number will be obtained.


2. If there is a denominator containing a variable, set the 
denominator equal to zero and solve this equation for the 
variable.  The real value (or these real values), if any are 
places where there is a vertical asymptote.  These must be 
deleted from the (, ) domain.

3. If there is an even root containing a variable, set the 
expression under the radical less than 0.  Solve this 
inequality. The solution set must be deleted from the 
(, ) domain.

Your problems:

A) 

This is case 2.  So we set the denominator = 0

  

This has no real solution, since the left side is always 
positive and can never equal 0.  So there are no vertical 
asymptotes, so we have nothing to delete from the (, )
domain. Therefore the domain is (, ). 



B) 

This is case 3, since square root is an even radical, so 
we solve the inequality:

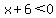 which has solution 

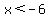Graphed on a number line this inequality is:

<==========o---------------------------------------------
 -9 -8 -7 -6 -5 -4 -3 -2 -1  0  1  2  3  4  5  6  7  8  9 

So we delete this from the (, )
domain below
 
<========================================================>
 -9 -8 -7 -6 -5 -4 -3 -2 -1  0  1  2  3  4  5  6  7  8  9

and that leaves this graph:

<----------@=============================================>
 -9 -8 -7 -6 -5 -4 -3 -2 -1  0  1  2  3  4  5  6  7  8  9  

which means that the domain of f(x) is [-6,).



C) k(t)=5t^2-6t+2

This is case 1.  There are no roots with even index or 
denominators containing a variable.  Therefore the solution 
is simply

<========================================================>
 -9 -8 -7 -6 -5 -4 -3 -2 -1  0  1  2  3  4  5  6  7  8  9

or (, )

  


D) 

This is case 2.  So we set the denominator = 0

  

This has one real solution, .  So there is a 
vertical asymptote at  so we must delete from the 
(, ) domain. So we delete 
this one point from the (, )
domain below:
 
<========================================================>
 -9 -8 -7 -6 -5 -4 -3 -2 -1  0  1  2  3  4  5  6  7  8  9

and that leaves this graph:
      
<======================o=================================>
 -9 -8 -7 -6 -5 -4 -3 -2 -1  0  1  2  3  4  5  6  7  8  9

and this in interval notation is

(, ) U (, )


E) 
This is case 1.  There are no roots with even index or 
denominator containing a variable.  Therefore the solution 
is simply

<========================================================>
 -9 -8 -7 -6 -5 -4 -3 -2 -1  0  1  2  3  4  5  6  7  8  9

or (, )

Edwin