|
Question 1208034: Find the range of f(x) = (x^2 + 2)/(x + 4) algebraically?
It is my understanding that the domain of f inverse is the range of f.
You say?
Found 2 solutions by ikleyn, math_tutor2020:
Answer by ikleyn(52794)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Find the range of f(x) = (x^2 + 2)/(x + 4) algebraically.
~~~~~~~~~~~~~~~~~~~
Let real number "t" belongs to the range. It means that
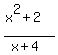 = t (1)
for some value of x. Step by step, reduce equation (1) to standard form quadratic equation = t (1)
for some value of x. Step by step, reduce equation (1) to standard form quadratic equation
 = =  , ,
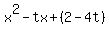 = 0. (2)
Equation (2) is a standard form quadratic equation = 0. (2)
Equation (2) is a standard form quadratic equation  = 0 with coefficients
a = 1, b = -t, c = 2-4t.
The condition that it has a real solution for = 0 with coefficients
a = 1, b = -t, c = 2-4t.
The condition that it has a real solution for  is this inequality for the discriminant is this inequality for the discriminant
 >= 0, or >= 0, or 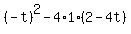 >= 0, or t^2 + 16t -8 >= 0.
The roots of this quadratic equation for t are >= 0, or t^2 + 16t -8 >= 0.
The roots of this quadratic equation for t are
 = =  = = 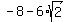 = -16.4853 (rounded) and = -16.4853 (rounded) and  = = 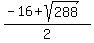 = =  = 0.4853 (rounded).
The discriminant is non-negative if and only if value of "t" is out of the roots' interval
t <= = 0.4853 (rounded).
The discriminant is non-negative if and only if value of "t" is out of the roots' interval
t <= 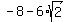 = -16.4853 or t >= = -16.4853 or t >=  =0.48528.
Therefore, equation (1) has a real solution if and only if =0.48528.
Therefore, equation (1) has a real solution if and only if  < t <= < t <= 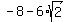 or or  <= t < <= t <  .
Thus the range of the function f(x) = (x^2 + 2)/(x + 4) is the union of these intervals ( .
Thus the range of the function f(x) = (x^2 + 2)/(x + 4) is the union of these intervals (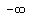 , ,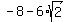 ] and [ ] and [ , , ).
ANSWER. The range of the function ).
ANSWER. The range of the function 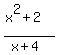 is the union of these intervals ( is the union of these intervals (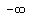 , ,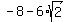 ] and [ ] and [ , , ). ).
Solved.
It is how to solve this problem using only elementary Algebra and without using Calculus.
This problem is a typical Math Olympiad level problem or Math circle level problem
for 9-th grades high school students, who just know Algebra, but still don't know Calculus.
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
You are correct.
The domain of the inverse is the range of the original function.
The domain and range swap places like this because x and y swap. After the swap the goal is to solve for y.
f(x) = (x^2+2)/(x+4)
y = (x^2+2)/(x+4)
x = (y^2+2)/(y+4) .... swapping x and y
x(y+4) = y^2+2
xy+4x = y^2+2
y^2-xy+2-4x = 0
To finish the process of solving for y, we use the quadratic formula.
a = 1
b = -x
c = 2-4x



The presence of "plus/minus" indicates the inverse isn't a function.
Notice how the original function f(x) fails the horizontal line test.
We want the radicand x^2+16x-8 to be nonnegative so we avoid the square root of a negative number.
Apply the quadratic formula to x^2+16x-8 = 0 to find the exact solutions are  and and 
Graph out y = x^2+16x-8
The graph is a parabola that opens upward.
The portion between the roots is when y < 0, so the radicand x^2+16x-8 is only nonnegative when  and and 
Therefore the range of the function f(x), as a set of inequalities, would be  or or 
The range in interval notation would be

The square brackets indicate we include both  and and  in the range. in the range.
Curved parenthesis are always with either infinity.
This is because we cannot reach infinity.
It's not on the number line. Rather it's a concept that represents going on forever in some direction.
If you prefer decimal approximations, then,
 and and  when rounding to 3 decimal places. when rounding to 3 decimal places.
The interval notation would then become (-infinity, -16.485] U [0.485, infinity)
The "U" symbol represents "set union". Informally it means "or", so the possible range of values is the interval (-infinity, -16.485] OR it's the interval [0.485, infinity)
Replace the word "infinity" with the infinity symbol if necessary.
|
|
|
| |