Question 1204559: Determine the intervals you would check to see when 
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
(1) Observe that f(1)=0, so x=1 is one root.
(2) Use synthetic division to find the remaining polynomial when the factor (x-1) is removed.
1 | 7 10 -11 -6
| 7 17 6
+-----------------
7 17 6 0
(3) Factor the remaining polynomial, 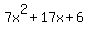 , using your favorite method; or find the other roots using the quadratic formula. , using your favorite method; or find the other roots using the quadratic formula.

The other two roots are x=-3/7 and x=-2.
The roots (smallest to largest) are now -2, -3/7, and 1; the intervals you need to check are
ANSWER: The intervals to check are (-infinity,-2), (-2,-3/7), (-3/7,1), and (1, infinity).
In fact, you don't need to check all those intervals to find where the function value is negative. You know that, with a cubic polynomial with positive leading coefficient and three distinct roots, the function value will be negative on (-infinity,-2) and (-3/7,1).
|
|
|