.
A curve has gradient function f'(x) = ax+1 where a is constant.
Find f(x) given that f(0) = 3 and f(3) = -3.
~~~~~~~~~~~~~~~~~~~
Since f'(x) = ax+1, we have f(x) = 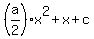 , where c is a constant term.
Since f(0) = 3 (given), it implies c= 3.
To determine value of "a", use the condition f(3) = -3. It gives you an equation
, where c is a constant term.
Since f(0) = 3 (given), it implies c= 3.
To determine value of "a", use the condition f(3) = -3. It gives you an equation
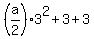 = -3,
or
9a/2 = - 9, i.e. a = -2.
ANSWER. f(x) =
= -3,
or
9a/2 = - 9, i.e. a = -2.
ANSWER. f(x) = 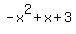 .
.
Solved.