|
Question 1180067: Please check the google document for the diagram!
a) Determine the area of the inscribed square as a function of x.
b) Determine the domain and range of the area function
c) Determine the perimeter of the inscribed square as a function of x
d) Determine the domain and range of the perimeter function!
https://docs.google.com/document/d/1Cl3HrcoR6jibNzxfDTIilS3imSplLY8nQUU0OpU9vLA/edit?usp=sharing
Found 2 solutions by MathLover1, ikleyn:
Answer by MathLover1(20850)   (Show Source):
Answer by ikleyn(52794)  (Show Source):
You can put this solution on YOUR website! .
The answer and the solution that you got from @MathLover1, are ABSURDIST.
Indeed, for the area of the inscribed square, she gives you A =  .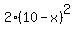
Substitute here x= 0: you will get A = 200 square units for the area of the inscribed square,
i.e. is TWO TIMES the area of the original square.
Similarly, for the perimeter of the inscribed square, she gives you P =  .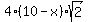
Substitute here x= 0: you will get P = 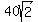 units for the perimeter of the inscribed square,
i.e. is 1.41 times the perimeter of the original square.
So, her solutions, OBVIOUSLY, are only good to throw them all to a TRASH BIN.
Ok, don't worry - - - you are in good hands. I came to bring a correct solution.
The square of the side of the inscribed triangle is
 =  +  =  =  .
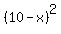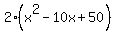THEREFORE, the area of the inscibed square
area = = = 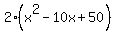. ANSWER
The perimeter is 4 (four) times the side lenght "a"
perimeter =  =  .
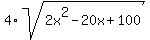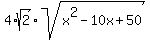Regarding the domain and the range of these functions, the question is posed in ambiguous way:
It has one answer for formal functions and another answer
if to base it on geometric meaning of variables.
THEREFORE, I prefer do not answer this question, until it is posed in a formally correct way.
|
|
|
| |
