SOLUTION: What is the midpoint of the line segment that has one endpoint as (9,-13) and the other endpoint as (-4,5)?

Algebra ->  Functions -> SOLUTION: What is the midpoint of the line segment that has one endpoint as (9,-13) and the other endpoint as (-4,5)?      Log On


   

Question 1170905: What is the midpoint of the line segment that has one endpoint as (9,-13) and the
other endpoint as (-4,5)?
Found 2 solutions by Alan3354, Edwin McCravy:
Answer by Alan3354(69443) About Me  (Show Source):
You can put this solution on YOUR website!
Makes no sense.

Answer by Edwin McCravy(20059) About Me  (Show Source):
You can put this solution on YOUR website!
Instead of doing your problem for you, I'll do another one that is exactly like
it step by step.  The problem I'll do for you is this:
What is the midpoint of the line segment that has one endpoint as (11,-15) and the
other endpoint as (-6,9)?
First I plot the points and draw the line:
  

Average the first coordinates, which are 11 and -6:
Add them (11)+(-6) = 5
Divide by 2.
Get 5%2F2
So 5%2F2 is the first coordinate of the midpoint.

Average the second coordinates, which are -15 and 9:
Add them (-15)+(9) = -6
Divide by 2.
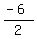Get %28-6%29%2F2, which reduces to -3
So -3 is the second coordinate of the midpoint.

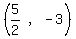So %28matrix%281%2C3%2C5%2F2%2C%22%2C%22%2C-3%29%29 is the midpoint of the
line segment.  Let's plot it as a check.  To plot the improper
fraction 5%2F2, we change it to mixed number 2%261%2F2.

  

That looks like the midpoint, So I think the correct answer to the problem
I worked is

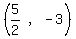%28matrix%281%2C3%2C5%2F2%2C%22%2C%22%2C-3%29%29

Now do your problem exactly the same way step by step.

Edwin