SOLUTION: Find the domain of f, the roots of f(x)=0, and determine the signs of f where f(x)= x^2-1/sqrt x+1 + sqrt x+1

Algebra ->  Functions -> SOLUTION: Find the domain of f, the roots of f(x)=0, and determine the signs of f where f(x)= x^2-1/sqrt x+1 + sqrt x+1      Log On


   

Question 115062: Find the domain of f, the roots of f(x)=0, and determine the signs of f where

f(x)= x^2-1/sqrt x+1 + sqrt x+1
Answer by solver91311(24713) About Me  (Show Source):
You can put this solution on YOUR website!
f%28x%29=%28x%5E2-1%29%2F%28sqrt%28x%2B1%29%2Bsqrt%28x%2B1%29%29

This function is undefined if x%2B1%3C=0, or putting a positive spin on the statement, the function is defined if and only if x%2B1%3E0 => x%3E-1. Therefore, the domain of the function is the interval (-1,infinity]

The zeros of the function can be seen readily if you factor the numerator and then rationalize the denominator.

f%28x%29=%28%28x%2B1%29%28x-1%29%29%2F2sqrt%28x%2B1%29
f%28x%29=%28%28x%2B1%29%28x-1%29sqrt%28x%2B1%29%29%2F2sqrt%28x%2B1%29sqrt%28x%2B1%29
f%28x%29=%28%28x%2B1%29%28x-1%29sqrt%28x%2B1%29%29%2F%282x%2B2%29

f%28x%29=0 iff x-1=0 or x%2B1=0 or sqrt%28x%2B1%29=0

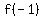x-1=0 iff x=1, so f%281%29+=+0 and 1 is a zero of the function.
x%2B1=0 iff x=-1, but -1 is not in the domain of the function, therefore f%28-1%29 is undefined (notice the open ended domain interval) and -1 is not a zero of the function.
sqrt%28x%2B1%29=0 iff x%2B1=0 => x=-1, and again, -1 is not in the domain.

Therefore the only zero of the function is 1.



As to the balance of your question, "determine the signs of f where..." Where what? Re-post with the complete question and someone will try to answer.