|
Question 1104434: Let f(x)=x^2 -1 and g(x)= x^2 - 2, for x has the domain of all real numbers
a. Show that (f ° g)(x)=x^4 - 4x^2 + 3.
do we do this by putting g(x) into f(x)? How would this look like?
b. How could I sketch the graph of (f ° g)(x), for 0 is < or equal to x < or equal to 2.25?
Could I plug this into my calculator to see the graph and just copy it from there?
c. The equation (f ° g)(x)=k has exactly two solutions, for x < or equal to x < or equal to 2.25. Find the possible values of k.
I have no idea how to do this part. Could you help?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! a. (f ° g)(x) =
b. Using a graphing calculator may be intended,
but you could still be expected to calculate and tabulate some values.
You may want to copy the shape, but make sure your graph goes through the zeros, maxima and minima of the function.
A graphing calculator can tells you where the zeros, the maxima, and the minima are.
The zeros of the function are the solutions to  . .
 --> --> --> --> --> --> --> --> --> --> --> --> . .
As we are working only where  , ,
That means the zeros of the function happen at
 and and  . .
If you were expected not to use a graphing calculator,
you would have to calculate derivatives, maxima and minima.

That first derivative is
positive for 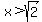 , meaning that the function increases in , meaning that the function increases in 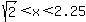 , and the derivative is , and the derivative is
negative for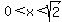 meaning that the function decreases there. meaning that the function decreases there.
The derivative is zero for  and and  . .
Those are the points where the slope of the graph is zero.
Because the function changes from decreasing to increasing at  , ,
that means that there is a minimum at  . .
At that point,
 , ,  , and , and   . .
We do not care what happens for  , ,
but (f ° g)(x) is an even function, symmetrical with respect to the y-axis, because (f ° g)(-x)=(f ° g)(x).
That ells us that at  there is a maximum. there is a maximum.
Two other points that should be plotted properly in the sketch of the graph are
(f ° g)(0) = 3 and (f ° g)(2.25) = 8.37890625 .
The second derivative,
 , ,
tells you where the inflection points are, and how the graph curves,
but maybe you are not expected to know that.
The graph with the important points in  circled looks like this: circled looks like this:
 , ,
c. The solutions to (f ° g)(x)=k are the x-coordinates of the points where y=(f ° g)(x)=k.
That is where the graph of  intersects the graph of intersects the graph of  . .
Looking at the graph,
you can see that for 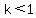 , , 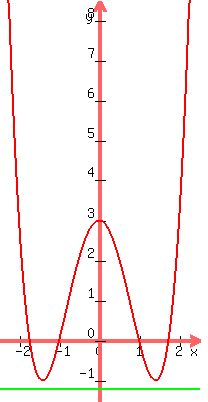 , ,
 is a horizontal line below the graph of the function, is a horizontal line below the graph of the function,
and (f ° g)(x)=k has no solution:
If k=-1, the equation is (f ° g)(x)=1, and it has only one solution for  , ,  . .
If   will cross the graph of will cross the graph of 
exactly twice in the interval  , ,  , ,
but if 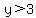 , ,  , ,
there will be only one solution in  . .
So, the possible values of k for (f ° g)(x)=k to have 2 solutions in  are are
 . .
|
|
|
| |