|
Question 1104321: 5. The graph of a function y= f(x), for -6 < or equal to x < or equal to -2.
The points (-6, 6) and (-2, 6) lie on the graph of f. There is a minimum point at (-4,0).
a. Write down the range of f.
b. Let g(x)=f(x-5).
Sketch the graph of g
c. Write down the domain of g.
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! The graph of a function y= f(x), for -6 < or equal to x < or equal to -2.
The points (-6, 6) and (-2, 6) lie on the graph of f. There is a minimum point at (-4,0).
-----
Plot those points and you will see a parabola will fit the points.
Because the minimum is at (-4,0), y = a(x+4)^2
Solve for "a" using (-2,6)
6 = a(2)^2
a = 3/2
Equation:: y = (3/2)(x+4)^2
---------------------------------
a. Write down the range of f.
Parabola opening up has range: 0<= y < oo
----------------------------------------
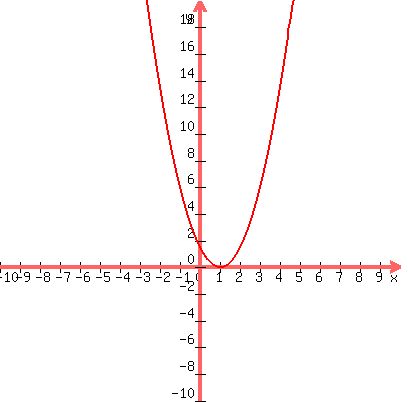
b. Let g(x)=f(x-5).
g(x) = f(x-5) = (3/2)(x-5+4)^2 = (3/2)(x-1)^2
Sketch the graph of g
------------------------
c. Write down the domain of g.
All Real Numbers
-----------
Cheers,
Stan H.
--------
|
|
|
| |