SOLUTION: Please help me with this question: If f(x) = x^2-x-1 and f[g(x)]=4x^2 + 10x + 5, find g(x). Any help will be greatly appreciated!

Algebra ->  Functions -> SOLUTION: Please help me with this question: If f(x) = x^2-x-1 and f[g(x)]=4x^2 + 10x + 5, find g(x). Any help will be greatly appreciated!       Log On


   

Question 1104188: Please help me with this question: If f(x) = x^2-x-1 and f[g(x)]=4x^2 + 10x + 5, find g(x).
Any help will be greatly appreciated!
Found 2 solutions by math_helper, KMST:
Answer by math_helper(2461) About Me  (Show Source):
You can put this solution on YOUR website!
I found it by trial and error, using hints from +f%28g%28x%29%29+=+4x%5E2+%2B+10x+%2B+5+
I assumed +g%28x%29+=+ax+%2B+b+
where a=2 because we need to end up with 4x%5E2
and 2ab - a = 10 —> a(2b-1) = 10 (EDIT: because a=2, this implies b=3, missed that earlier)
Another hint/constraint is that +b%5E2+-+b+-+1+=+5+
I found a=2 and b=3 works. +g%28x%29+=+2x+%2B+3+

—
Of course, this worked out because I guessed the proper form for g(x).
Maybe another tutor may have a more structured method. I'm often amazed at the talent base here.
—

Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
There has to be a better way, but here it goes.
If f[g(x)] =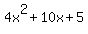4x%5E2+%2B+10x+%2B+5
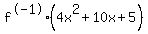
g%28x%29=f%5E-1{ f[g(x)] } =f%5E-1%284x%5E2+%2B+10x+%2B+5%29
To find the inverse function of f%28x%29=x%5E2-x-1 , graph%28300%2C300%2C-5%2C5%2C-2%2C8%2Cx%5E2-x-1%29 ,
we exchange x and y in
y=x%5E2-x-1 to get x=y%5E2-y-1 and then solve for y .
We get y=%281+%2B-+sqrt%284x%2B5%29%29%2F2 , .
That is really two functions,
and when working with real numbers,
it is only defined for x%3E=-5%2F4 ,
but we continue, to see what we can get.
If f%5E-1%28x%29=%281+%2B+sqrt%284x%2B5%29%29%2F2
.
So, highlight%28g%28x%29=2x%2B3%29 is a solution.

NOTES:
1) There was no problem with f%5E-1%28x%29=%281+%2B+sqrt%284x%2B5%29%29%2F2 being defined only for x%3E=-5%2F4 ,
because we are going to apply it to
4x%5E2+%2B+10x+%2B+5=%282x%2B5%2F2%29%5E2-5%2F4%3E=-5%2F4 .
2)
Would we get another solution out of f%5E-1%28x%29=%281-sqrt%284x%2B5%29%29%2F2 ?
Let's check.
In that case, we would have
.
If f%28-2x-2%29=4x%5E2+%2B+10x+%2B+5 ,
f%5E-1%284x%5E2+%2B+10x+%2B+5%29=-2x-2 could be another g%28x%29 .
Let's see.
f%28-2x-2%29=%28-2x-2%29%5E2-%28-2x-2%29-1=4x%5E2%2B4x%2B1%2B2x%2B2-1=4x%5E2%2B6x%2B1
No. It does not work.