|
Question 1103955: Suppose you invest $1600 at an annual interest rate of 4.6% compounded continuously. How much will you have in the account after 4 years?
Can you explain?
Answer by math_helper(2461)   (Show Source): (Show Source):
You can put this solution on YOUR website! 
F=future value
P=present value
r=annual interest rate
t=number of years

You would have about $1923.23 after 4 years.
——
To explain it: Look at the discrete compound interest formula:

where F,P,r, and t are as above
n = number of compounding periods per year
Clearly, if n=1 you get your interest once per year (in this case 0.046*1600 = 73.60, looking at the FIRST year only to illustrate the point).
—
If n=2 you get interest twice per year, however, the calculated rate is cut in half for each payment. You still end up better off at the end of the first year than in the n=1 case. This is because the interest you've earned after 6 months ( 0.046/2 * 1600 = 36.80) has earned you a little bit of interest for the 2nd 6 months (0.046/2 * 1636.80 = 37.64). For n=2, the interest earned for the first year is 36.80+37.64=74.44, which is greater than the n=1 case of 73.60 (yes, by a measly 0.84, but when principal values are larger and interest rates are higher, those differences are larger too).
—
Now, if n=2 is better than n=1 then why not just keep making n bigger? Sure, all other things being equal, if given the choice of annual compounding vs 6 months vs 3 months vs weekly vs daily, you'd want the most frequent compounding. But, some bad news: you eventually hit a limit. That limit is when n is so big you are continuously compounding the interest.
—
Mathematically:

Letting 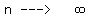 , and substituting u=n/r (so n=u*r) gives , and substituting u=n/r (so n=u*r) gives
Lim 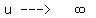 
Lim 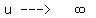 
Now we notice Lim 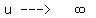 
so Lim 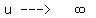 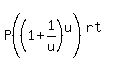 is is 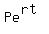
and 
|
|
|
| |