|
Question 1100477: Nour drove from the Dead Sea up to Amman, and her altitude increased at a constant rate.
When she began driving, her altitude was 400 meters below sea level.
When she arrived in Amman 2 hours later, her altitude was 1000 meters above sea level.
Let A(t) denote Nour's altitude relative to sea level A (measured in meters) as a function of time t (measured in hours).
Write the function's formula.
Found 5 solutions by Alan3354, richwmiller, greenestamps, josgarithmetic, ikleyn:
Answer by Alan3354(69443)   (Show Source):
Answer by richwmiller(17219)  (Show Source):
You can put this solution on YOUR website! Your numbers are coming out three times
400 is coming out as 400400400
2 is coming out as 222
1000 is coming out as 100010001000
A is appearing as AAA
t is appearing as ttt
the points are
(0,-400)
(2,1000)
I was trying to use pluggable solvers presented by other tutors but they didn't work.
Yes, I missed below sea level. I was concentrating on clearing up the weird numbers.
Alan's comment was when the problem had numbers such as 400400400 and 100010001000
Answer by greenestamps(13200)  (Show Source):
You can put this solution on YOUR website!
Not only confusing, but...
(1) your graphs aren't showing what you wanted them to (yes, I too am still learning how to make graphs the way I want them on this web site...!); and
(2) the starting point is 400 meters BELOW SEA LEVEL, so (0,-400) instead of (0,400)
Answer by josgarithmetic(39620)  (Show Source):
You can put this solution on YOUR website! Points (t, A(t)) are (0, -400) and (2, 1000).
Change of altitude with time was described as constant.
and the vertical axis intercept is given.
Answer by ikleyn(52799)  (Show Source):
You can put this solution on YOUR website! .
Wikipedia article ( https://en.wikipedia.org/wiki/Dead_Sea ) says
The Dead Sea is a salt lake bordered by Jordan to the east and Israel and Palestine to the west.
Its surface and shores are 430.5 metres (1,412 ft) below sea level, Earth's lowest elevation on land.
The formula for Nour's altitude, that the problem is asking for, is
A(t) = -400 +  .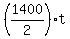
Indeed, it is a linear function of t (t is time in hours), which has the value of -400 meters at t= 0 (when Nour started her move)
and the value of 1000 meters at t = 2 hours, when Nour arrived to Amman.
So the formula satisfies all conditions imposed to the function.
Solved.
|
|
|
| |
