|
Question 1096250: A container contains 12 Diesel engines. The company chooses 6 at random, and will not ship the container if any of the engines chosen are defective. Find the probability that a container will be shipped even though it contains 2 defectives if the sample size is 6.
Please explain in Full Detail because I have no clue how to solve, even though Iíve watched videos, etc.
What is the number of successes in the population?
What is the number of successes in the sample?
How do you determine each?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! Math is not a collection of problem-solving recipes and "facts" to be memorized. Most of the tricks smarter people have figured out, you can figure out by yourself, because it just makes sense. The more clever tricks will make be understood and remembered, once you are shown how people figured them out before.
Let us say you have a container with  two,faulty engines and two,faulty engines and  good engines. Maybe you could label the engines with numbers from 1 to 12, and maybe the faulty engines could have numbers 11 and 12. good engines. Maybe you could label the engines with numbers from 1 to 12, and maybe the faulty engines could have numbers 11 and 12.
If the engines in the container are so labeled, you could describe a set or
list of engines chosen for testing as
1,2,3,4,5,6 or 6,5,1.2,4,3 or 2,5,6,8,10,12
or some list like that.
How many such lists could there be? The number of lists you could make is
 , because there would be 12 possible choices for the first number in the list, 11 for the second, 10 to the third, and so on. , because there would be 12 possible choices for the first number in the list, 11 for the second, 10 to the third, and so on.
The same reasoning tells you that there would be 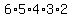 lists for each set of 6 numbers, because the same 6 numbers can be listed in that many orders. lists for each set of 6 numbers, because the same 6 numbers can be listed in that many orders.
Putting those two reasoned findings together, you see that there are
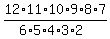 different possible sets of 6 engines that can be chosen for testing. different possible sets of 6 engines that can be chosen for testing.
You have a number of sets, and a number of lists. Your teacher talked about combinations and permutations. Maybe you need to remember those "vocabulary words" for the test. I say that for this problem words do not matter. All those lists and sets are equally likely to be chosen for testing when the inspector radomly choses 6 engines to be tested. That is what matters.
Of all the possible sets/lists of 6 engines, how many could have 6 good engines?
Out of the 10 good engines in the container, you could make
 different sets of 6 good engines, different sets of 6 good engines,
or  lists of 6 good engines lists of 6 good engines
The sets or lists with 6 good engines are a fraction of all the possible sets or lists of 6 engines. If the inspector randomly picks one of those good sets or lists of engines to test,
the container ships.
The probability of that happening is the fraction of good 6-engine sets (or lists) out of all possible sets (or lists) of 6 engines.
That fraction is
 (the fraction of sets) or (the fraction of sets) or
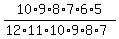 (the fraction of lists). (the fraction of lists).
It is the same,number, of course. It is
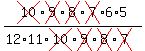 = = = =
|
|
|
| |