Given h(x), find a pair of functions f and g such that h(x) = fgg(x):
h(x) = square root 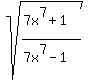 .
Pick g(x) as any expression in x from the whole expression
.
Pick g(x) as any expression in x from the whole expression
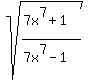 such that if you were to substitute u for that expression,
there will be no x's left.
-----------------
Suppose we pick u to be
such that if you were to substitute u for that expression,
there will be no x's left.
-----------------
Suppose we pick u to be 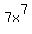 , then we replace both
the
, then we replace both
the 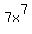 's by u and get
's by u and get
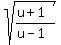 g(x) is simply equal to what we picked u to be, that is,
g(x) =
g(x) is simply equal to what we picked u to be, that is,
g(x) = 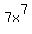 To get f(x) we substitute x for u in
To get f(x) we substitute x for u in
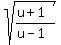 and get
and get
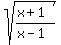 So
f(x) =
So
f(x) = 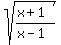 g(x) =
g(x) = 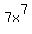 Checking:
h(x) = fgg(x) = f(g(x)) = f(
Checking:
h(x) = fgg(x) = f(g(x)) = f(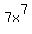 ) =
) = 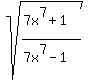 .
Edwin
.
Edwin