|
Question 1087149: Consider the function f(x)= |x-1|+|x-2|
Show that f(x)= -2x+3, if x ≤ 1
1 if 1 < x < 2
2x-3 if x ≥ 2
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! Given function: 
Let  and and 
That means 
We can write the absolute value functions, g(x) and h(x), into piecewise function form
For g(x) we have

which basically says  if if  OR OR  if if 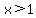
and for h(x) we have

which basically says  if if  OR OR  if if 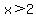
We have three intervals
Interval A: the interval where 
Interval B: the interval where 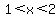
Interval C: the interval where 
Focus on interval A. Since  here this means that here this means that  and and 
Therefore,  when when 
In short,  when when 
Now move onto interval B. We have 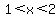 . This interval will have us use g(x) = x-1 and h(x) = -(x-2). Add the functions to get . This interval will have us use g(x) = x-1 and h(x) = -(x-2). Add the functions to get
 when when 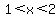
In short,  when when 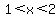
Finally interval C. Now  . For this interval . For this interval  and and 
So,  when when 
In short,  when when 
To recap, we found the following
 when when 
 when when 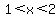
 when when 
Which can be combined to form the piecewise function

So this proves that overall,  for all real numbers x for all real numbers x
As visual confirmation, here is a graph showing a side by side comparision of f(x) and k(x). I let f(x) = |x-1|+|x-2| while k(x) is the piecewise function equivalent form. The two function curves are blue and brown respectively. As you can see, they are identical. If you laid them on the same xy coordinate system then you'd have the same graph. One function curve would overlap the other perfectly.
Note: The graph was created with GeoGebra (free graphing software).
|
|
|
| |