|
Question 1075366: Given the graph below, write the radical function for f(x).
These are the coordinates that I took from my homework:
(-2,3)(-1,2)(2,1)(7,0)
I am sorry if I don't have a graph to place on this website, but radical function means A function that contains a radical expression with the independent variable in the radicand. Also a radicand is the number or expression inside a radical symbol.
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! If your graph has only those 4 points,
it is a cumbersome problem.
I would start with  ,
would solve for a, b, and c,
and then would solve for y.
Substituting the coordinates of (7,0),
you get  .
Point (2,1) gives you
 --->  .
Point (-1,2) gives you
 --->
Solving  , you get
 and  .
So,  fits 3 of the points.
The fourth point confirms it.
Solving  for y, you get
 ,
which simplifies to  .
That is 2 choices.
Your function increases as x increases, so it is
 .
If your graph is a continuous curve that looks like this:
you would think that it looks just like  ,
but translated 2 units to the left and 3 units up.
That would make it .
I would bet that is what the teacher wants, and if so,
there should be something to tell you that the function was a transformed  .
At least you should think there is
an  inside the squate root,
because the function is not defined for  <--->  .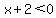
Then you would also think there is a positive coefficient
multiplying the square root, because y increases with x,
and a 3 added to the square root term,
because the graph starts at y=3.
|
|
|
| |
