|
Question 1074717: Let A={1,2,3,4,5}.
(a) How many total functions f∶ A→A are there?
(b) How many of the functions in (a) are one-to-one?
Can someone please explain on how to start and solve these type of question? Thank you!
Found 2 solutions by KMST, ikleyn:
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! (a) A function f: A --> A assign to each element of A a unique mate in A.
so, 1 would be assigned one and only one mate from A,
and so would 2, but it could even be the same mate.
For example a function could pair each element from A with 1:
 . .
With 5 choices of mate for every one of the 5 elements of A.
For each of the 5 choices for  , ,
you have 5 choices for  , making , making  choices so far. choices so far.
Then, for each on one of those  choices, choices,
you couls till make 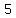 , and so on. , and so on.
That gives you  different functions. different functions.
(b) A one-to-one function would assign to each element a different mate.
Usually marriage is a one-to-one function, although some countries do no make it so.
To define a one-to one function, you could start by picking a mate for 1, and write  . .
You have  choices to fill that blank. choices to fill that blank.
Next you may want to pick a mate for 2, but now you only have  choices for choices for  . .
after that you would have  choices, then choices, then  , and then , and then  . .
The number of possible functions you could choose is
 . .
Your teacher may say something like
(a) is a case of permutations with repetition,
(b) is a case of permutations without repetition.
I say, imagine this is real life.
Remember the "math vocabulary words" for as long as required, if required,
but what you really need is thinking with your own head,
and understanding a problem to solve it.
Answer by ikleyn(52798)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Let A={1,2,3,4,5}.
(a) How many total functions f∶ A→A are there?
(b) How many of the functions in (a) are one-to-one?
Can someone please explain on how to start and solve these type of question? Thank you!
~~~~~~~~~~~~~~~
The short explanation is this:
(a) Every function f: A --> A correlates some values of the set A to each element of the set A.
Every function f: A --> A is such a correlation.
Function f can correlate ANY of 5 values 1, 2, 3, 4 and/or 5 to the element "1" : FIVE options.
Function f can correlate ANY of 5 values 1, 2, 3, 4 and/or 5 to the element "2" : FIVE options.
. . . and so on till 5.
In all, there are 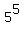 different functions.
(b) One-to-one function in this context is simply a permutation ("without repetition").
The number of permutations of 5 objects is 5! = 120 - very well known fact. different functions.
(b) One-to-one function in this context is simply a permutation ("without repetition").
The number of permutations of 5 objects is 5! = 120 - very well known fact.
Solved.
|
|
|
| |