|
Question 1061077: Find the domain of the rational function.
f(x) = 2x^2-4 / 3x^2+6x-45
a. {x|x ≠ -3, x ≠ 5}
b. {x|x ≠ 3, x ≠ -5}
c. all real numbers
d. {x|x ≠ 3, x ≠ -3, x ≠ -5}
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! The rational function should be written as
f(x) = (2x^2-4) / (3x^2+6x-45) =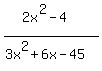 , ,
with brackets to indicate that it is a quotient of two polynomials that must be evaluated before dividing,
because I am pretty sure that
f(x) = 2x^2-4 / 3x^2+6x-45 =   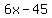 is not what was meant. is not what was meant.
TIPS:
1) For multiple choice questions,
when you do not need to "show your work,"
you do not need to calculate much.
2) Rational functions are defined everywhere except where the denominator is zero,
and polynomials have an even number of real zeros equal or less than their degree.
3) Polynomials are defined everywhere (meaning that their domain is all the real numbers),
so if a polynomial is positive for a certain value of  , ,
and is negative for another value of  , ,
that polynomial is zero for some in-between value of  . .
With the tips above, I first realize that the denominator,  , is a polynomial of degree 2, , is a polynomial of degree 2,
so it may have two real zeros, or no real zeros.
Then I realize that since  and and  , ,
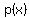 must have one real zero between must have one real zero between  and and  , ,
but since real zeros come in pairs, it must have two real zeros.
That eliminates answers c an d,
so if 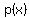 is zero for is zero for  , the answer must be b, , the answer must be b,
and otherwise the answer is a.
 , so the answer is , so the answer is  . .
If it were not multiple choice answers to give you clues,
you would have to find the zeros (if any) of the denominator.
To do that you would try to solve  by whatever method was easier for you. by whatever method was easier for you.
If you are good at factoring polynomials, you are in luck, because this one factors easily.
In fact, you may have just written
 , ,
and that shows that the denominator is zero
for  <--> <--> and for and for  <--> <--> . .
That tells you  and and  are not part of the domain of are not part of the domain of  , ,
and that the answer is b.
Otherwise, and in case where real zeros do not exist or are irrational,
you may be tempted to solve the equation  using the quadratic formula. using the quadratic formula.
Solving  using the quadratic formula is not fun. using the quadratic formula is not fun.
Since  , solving , solving  is a smarter idea is a smarter idea
that leads to less complicated calculations.
Using the quadratic formula,  , ,

would give you
 and and  . .
|
|
|
| |