|
Question 1051143: Find the dimensions of the rectangular corral split into 2 pens of the same size producing the greatest possible enclosed area given 600 feet of fencing. (Assume that the length is greater than or equal to the width.)
Answer by ikleyn(52794)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Find the dimensions of the rectangular corral split into 2 pens of the same size producing the greatest possible
enclosed area given 600 feet of fencing. (Assume that the length is greater than or equal to the width.)
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
I prepared the Figure on the right to show how I see and understand
the condition.
In the Figure, L means the length and W means the width of each pen.
So, we have 3 pieces of fencing of the length L each and 4 pieces
of fencing of the length W each.
Then we have this equation
3L + 4W = 600,
from which we have W = 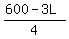 . .
|
 Figure.
Figure.
|
Next, the combined area of the two corals is
A = L*2W =  = = 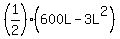 = = 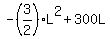 ,
and we have to find the length L in a way to maximize the area A, i.e. maximize the quadratic function
A = ,
and we have to find the length L in a way to maximize the area A, i.e. maximize the quadratic function
A = 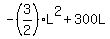 .
Now let me remind you that, if you have a quadratic function f(x) = .
Now let me remind you that, if you have a quadratic function f(x) =  of the general form,
then it reaches the maximum/minimum at x = of the general form,
then it reaches the maximum/minimum at x = 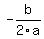 .
For our situation, a = .
For our situation, a =  and b = 300.
Therefore, the maximum is at L = - and b = 300.
Therefore, the maximum is at L = - 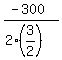 = = 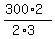 = 100.
Thus the area get a maximum at L = 100 feet.
Then W = = 100.
Thus the area get a maximum at L = 100 feet.
Then W = 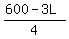 = = 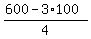 = 75 feet.
Answer. The area is maximal at L = 100 feet and W = 75 feet.
Then the area of one coral is 100*75 = 7500 square feet.
The combined area of the two corals is twice this value, i.e. 15000 square feet. = 75 feet.
Answer. The area is maximal at L = 100 feet and W = 75 feet.
Then the area of one coral is 100*75 = 7500 square feet.
The combined area of the two corals is twice this value, i.e. 15000 square feet.
The plot below confirms this solution.

Plot f(L) = 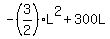
|
|
|
|
| |