SOLUTION: A function f(x) contains points A, B, C, and D A(-2,0) B(0,2) C(3,-1) D(4,4) The function is transformed to create g(x) Such that g(x) = f (1/2 x) - 4. Complete the table

Here are the 5 rules for what happens to each point of a 
graph when x is replaced by something in the right side 
of the equation. Assume in all cases that k is a positive 
number.

1. Replacing x by -x
   [Reflects graph across the y-axis]

2. Replacing x by (x+k)
   [Shifts graph k units left] 

3. Replacing x by (x-k).
   [Shifts graph k units right]    

4. Replacing x by kx, where k > 1
   [Shrinks graph horizontally by a factor of 1/k. 

5. Replacing x by 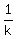x, where k > 1
   [Stretches graph horizontally by a factor of k.


Here are the 5 rules for what happens to a graph when 
something is done to the right side of the equation:

 6. Multiplying the right side of the equation by -1
    [Reflects graph across the x-axis]

 7. Adding k to the right side of the equation
    [Shifts graph k units upward]

 8. Subtracting k from the right side of an equation
    [Shifts graph k units downward]
                   
 9. Multiplying the right side of the equation by k, where k > 1
    [Stretches graph vertically by a factor of k]

10. Multiplying the right side of the equation by k, where 0 < k < 1
    [Shrinks graph vertically by a factor of 1/k]

-----------------------------

We are to find .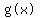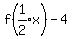

Using rule 5, replacing x in the right side of the equation of f(x)
by 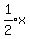 would stretch horizontally by a factor of 2,

So A(-2,0) would stretch horizontally to (-2*2,0) = (-4,0),
   B(0,2) would stretch horizontally to (0*2,2) = (0,2)
   C(3,-1) would stretch horizontally to (3*2,-1) = (6,-1)
   D(4,4) would stretch horizontally to (4*2,0) = (8,0)

Then by rule 8, subtracting 4 from the right side of 
would shift vertically DOWNWARD by 4 units

So (-4,0) would shift vertically downward to A'(-4,0-4) = A'(-4,-4)
   (0,2) would shift vertically downward to B'(0,2-4) = B'(0,-2)
   (6,-1) would shift vertically downward to C'(6,-1-4) = C'(6,-5)
   (8,0) would shift vertically downward to D'(8,0-4) = D'(8,-4)

Edwin