|
Question 1044892: Kindly help me solving it i tried my best but I couldn't
lim 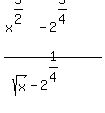 is equal to is equal to
x➡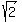
a)1/10
b)10
c)20
d)none of these
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! Your expression/function of  is is
  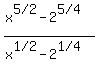  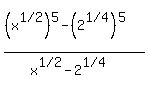 . .
Looks complicated, but it can be simplified.
We need a change of variable, so we do not have to struggle with those fractional exponents.
If I rewrite your function with  , ,
and define a constant  , ,
 looks as simple as looks as simple as  , a rational function of , a rational function of  , ,
with the constant  --> --> . .
Now, if 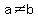 <---> <---> 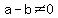 , ,
we know a way to transform that rational function into a polynomial:
 for for 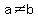 . .
Now  , and , and 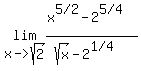 
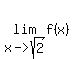  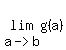  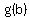  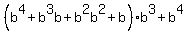  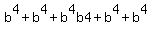  
NOTES:
1) Your instructor may favor  rather than rather than  as the variable for a change of variable. as the variable for a change of variable.
I chose  because it should remind you of what you learned in algebra and/or "pre-calculus". because it should remind you of what you learned in algebra and/or "pre-calculus".
2) You may remember from algebra/pre-calculus that
 , and , and
 . .
You should not be surprised to find out that
 <---> <--->  . .
Alternately, you may recognize 
as the sum of the first five terms of a geometric sequence
with first term 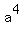 and common ratio and common ratio  , ,
and that sum would be 
|
|
|
| |