SOLUTION: The solution set in interval notation of the inequality (4/x-1)>(3/x) is: A) (-∞, 0)U(0, ∞) B) (-3, 0)U(1, ∞) C) (-∞, -3)U(0, 1) D) (-∞, -3) E)

Algebra ->  Functions -> SOLUTION: The solution set in interval notation of the inequality (4/x-1)>(3/x) is: A) (-∞, 0)U(0, ∞) B) (-3, 0)U(1, ∞) C) (-∞, -3)U(0, 1) D) (-∞, -3) E)      Log On


   

Question 1006237: The solution set in interval notation of the inequality (4/x-1)>(3/x) is:
A) (-∞, 0)U(0, ∞)
B) (-3, 0)U(1, ∞)
C) (-∞, -3)U(0, 1)
D) (-∞, -3)
E) (0,1)
Found 2 solutions by MathLover1, josgarithmetic:
Answer by MathLover1(20850) About Me  (Show Source):
You can put this solution on YOUR website!
%284%2F%28x-1%29%29%3E%283%2Fx%29+...........cross multiply
4%2Ax%3E3%28x-1%29+
4%2Ax%3E3x-3
4%2Ax-3x%3E-3
x%3E-3
since we have denominators %28x%29+ and x-1=>x%3C%3E0 and x%3C%3E1
so, your solution is
-3%3Cx%3C0=>(-3, 0)
and x%3E1=>(1, infinity)

or (-3, 0) U (1, infinity)

+graph%28+600%2C+600%2C+-10%2C+10%2C+-10%2C+10%2C4%2F%28x-1%29%2C3%2Fx%29+


Answer by josgarithmetic(39618) About Me  (Show Source):
You can put this solution on YOUR website!
Ambiguous inequality, maybe really meant as 4/(x-1)>3/x,

4%2F%28x-1%29-3%2Fx%3E0

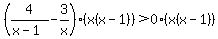
%284%2F%28x-1%29-3%2Fx%29%28x%28x-1%29%29%3E0%28x%28x-1%29%29

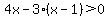
4x-3%28x-1%29%3E0

4x-3x%2B3%3E0

x%2B3%3E0

highlight%28x%3E-3%29 which is the interval notation form, (-3, infinity).
Be aware, a critical value is x at 0. The inequality will be UNDEFINED for x=0.
Another critical value is x at 1; the inequality is UNDEFINED for x=1.



You will make better sense of the choices given if your inequality really is exactly as it was shown in your question: 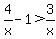4%2Fx-1%3E3%2Fx, and the only critical value would be x at 0 being the undefined value for x in the inequality.
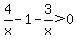
4%2Fx-1-3%2Fx%3E0
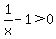
1%2Fx-1%3E0
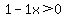
1-1x%3E0
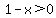1-x%3E0.
Now the critical values of x are 0 and 1.
The intervals on x to check are (-infinity,0), (0,1), and (1, infinity).

--
One should get all expressions onto one side with 0 on the other side before further simplifying because the denominators may be positive OR negative, affecting the order when performing the multiplication for the order relationship.