SOLUTION: Plz help me to explain the range of this equation. {f(x)=1�x^2-2x-3}

Click here to see ALL problems on Functions

Question 1000359: Plz help me to explain the range of this equation. {f(x)=1�x^2-2x-3}
Found 2 solutions by solver91311, Theo:
Answer by solver91311(24713) (Show Source):
You can put this solution on YOUR website!

I presume you mean

It will be helpful to first factor the quadratic in the denominator so that you can find the zeros of the denominator and thereby know the boundaries of the region in which the denominator is negative and the regions where it is positive.

The values that make the denominator zero are the vertical asymptotes of the graph. Since we know that the denominator is positive on one side of an value that makes the denominator zero and negative on the other side, we know that the function is going to take off toward either positive or negative infinity depending which side of the zero you are on.

When becomes very large in either the positive or negative direction, the denominator will become very large, and, therefore, this function will get closer and closer to zero, but will never actually be zero. That gives us the positive part of the range -- the open interval 0 to infinity.

The last question we have to answer is what is the highest value the function will reach when the denominator value is negative. For that, you need to find the value of the denominator at the vertex of the parabola represented by the denominator and then find the reciprocal of that value. Then the other half of your range will be the half-closed interval from negative infinity to the largest negative function value.

John

My calculator said it, I believe it, that settles it

Answer by Theo(13342) (Show Source):
You can put this solution on YOUR website!
the denominator of that equation is x^2 - 2x - 3.

we'll call that g(x).

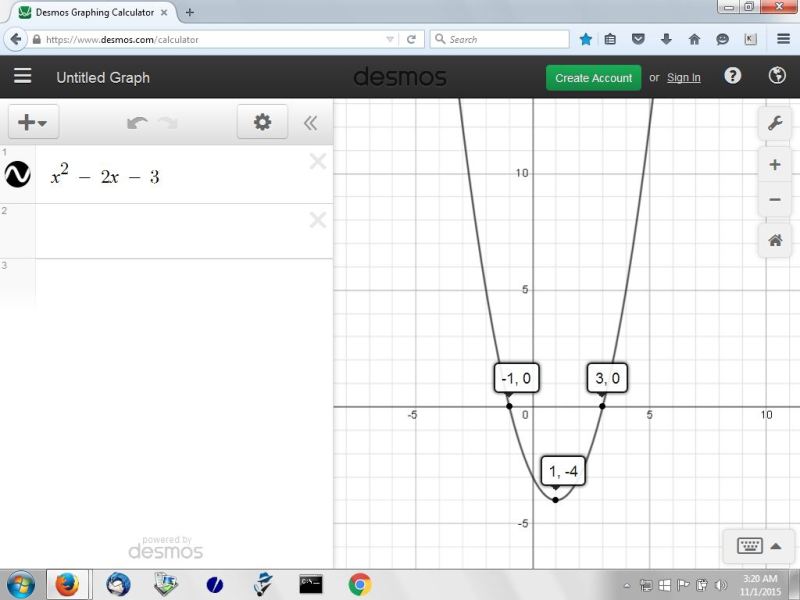
g(x) is a quadratic equation that can be solved to provide the following information:

the graph crosses the x-axis at x = -3 and x = 1.
the minimum point on the graph is at (1,-4)
the graph is positive from x > - infinity to x < -3.
the graph is negative between x > -3 to x < 1.
the graph goes positive again between x > 1 to x < infinity.

the range of g(x) is all values of y greater than or equal to -4.

f(x) is equal to 1 / g(x).

f(x) is therefore the reciprocal of g(x).

when g(x) is going towards positive infinity, f(x) is going towards 0 from the positive side.
when g(x) is going towards negative infinity, f(x) is going towards 0 from the negative side.
when g(x) is going towards 0 from the positive side, f(x) is going towards positive infinity.
when g(x) is going towards 0 from the negative side, f(x) is going towards negative infinity.

every value of f(x) is going to be equal to 1 divided by every value of g(x).

when g(x) is at -4, f(x) will be at -.25.

the range of f(x) will be all values of y > 0 and all values of y <= -.25.

this can be seen on the graphs.

there are 3 graphs:

first graph is graph of g(x).
second graph is graph of f(x).
third graph is graph of f(x) and g(x) on the same graph.

in the third graph, the values of f(x) and g(x) are shown at x = -3, x = 1, and x = 5, so you can see that the values of f(x) are the reciprocal of the values of g(x) at those values of x.

this occurs at all values of x, but only those 3 values of x are shown for clarity.