SOLUTION: Can you help me please to solve this question:find the rational function F:ℝ→ℝ with range f:(ℝ)= [0,1] .(thus f(x)=p(x)/Qx) for all xεℝ for suita

Algebra ->  Functions -> SOLUTION: Can you help me please to solve this question:find the rational function F:ℝ→ℝ with range f:(ℝ)= [0,1] .(thus f(x)=p(x)/Qx) for all xεℝ for suita      Log On


   

Question 807888: Can you help me please to solve this question:find the rational function F:ℝ→ℝ with range f:(ℝ)= [0,1] .(thus f(x)=p(x)/Qx) for all xεℝ for suitable polynomial P and Q where Q has no real root). you should justify your choice of f clearly. [10 marks]. I’m really stuck, i dont even know how to start it. it would be so nice if you can help. thank you
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
I assume this is pre-calculus and I cannot mention derivatives.

The first 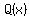Q%28x%29 with no real root I can think of is
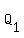Q%5B1%5D%28x%29=x%5E2%2B1 .
It is always positive, with a minimum at (0,1).
Not bad for our first try.

The simplest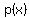p%28x%29 I can think of is p%5B1%5D%28x%29=1 .
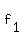f%5B1%5D%28x%29=1%2F%28x%5E2%2B1%29 is a bell shaped curve with a maximum at (0,1)
and x=0 for a horizontal asymptote.
Its range is (0,1] because 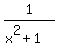1%2F%28x%5E2%2B1%29 is never zero.

If the range must include 0 and 1, we must keep on thinking.
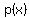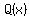A bound range means the grade of p%28x%29 cannot be grater than the grade of Q%28x%29.
To have p%28x%29%2F%28x%5E2%2B1%29%3E=0 , we need p%28x%29%3E=0.
A first degree polynomial would not do, because polynomials of odd degree have at least one real root where they change sign.
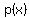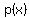For p%28x%29 we may want a quadratic polynomial that does not change sign but has a zero. That means a p%28x%29 with a double root.
We cannot use x%5E2, because while that adds f%280%29=0 to the range, it eliminates 1 from the range.

We want the zero at x%3C%3E0 .
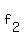Making p%5B2%5D%28x%29=%28x-1%29%5E2 ensures that p%5B2%5D%28x%29%3E=0 with p%5B2%5D%281%29=0 and f%5B2%5D%281%29=0 .
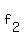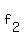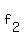The function f%5B2%5D%28x%29=%28x-1%29%5E2%2F%28x%5E2%2B1%29%3E=0 with f%5B2%5D%280%29=1 and f%5B2%5D%281%29=0 looks promising, but we need to make sure that f%28x%29%3C=1 , at all times.
Obviously 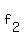f%5B2%5D%28x%29=%28x-1%29%5E2%2F%28x%5E2%2B1%29 fails at that,
because 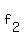f%5B2%5D%28-1%29=%28-1-1%29%5E2%2F%28%28-1%29%5E2%2B1%29=%28-2%29%5E2%2F%281%2B1%29=4%2F2=2

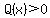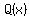With two quadratic polynomials p%28x%29%3E=0 , and Q%28x%29%3E0 ,
and the minimum of Q%28x%29 do not happen at the same x may have a maximum M%3E0.
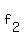If f%5B2%5D%28x%29=%28x-1%29%5E2%2F%28x%5E2%2B1%29 has a maximum M%3E0 ,
%28x-1%29%5E2%2F%28x%5E2%2B1%29%3C=M --> %28x-1%29%5E2%2F%28M%28x%5E2%2B1%29%29%3C=1
and f%5B3%5D%28x%29=%28x-1%29%5E2%2F%28M%28x%5E2%2B1%29%29%3C=1 is our answer.
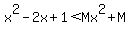%28x-1%29%5E2%2F%28x%5E2%2B1%29%3C=M <--> %28x-1%29%5E2%3C=M%28x%5E2%2B1%29 <--> x%5E2-2x%2B1%3CMx%5E2%2BM <--> x%5E2-Mx%5E2-2x%2B1-M%3C=0 <--> %281-M%29x%5E2-2x%2B%281-M%29%3C=0
That is true when M=2 .
-x%5E2-2x-1=-%28x-1%29%5E2 -x%5E2-2x-1%3C=0 <--> x%5E2-2x%2B1%3C=2x%5E2%2B2 <--> %28x%5E2-2x%2B1%29%2F%282x%5E2%2B2%29%3C=1
highlight%28f%28x%29=%28x-1%29%5E2%2F%282x%5E2%2B2%29%29 is our answer.