s(x) = 
Two things to remember about domains.
1. Denominators must never equal to zero.
2. What square roots are taken of must never be negative.
First we must make sure that what the square root is taken of,
which is 
, must never be negative. So we
set it greater than 0:
We find the critical values by setting numerator and denominator
equal to 0
3 - x = 0 and solving gives critical value x = 3
3x + 2 = 0 and solving gives critical value x = 
So we mark those points on a number line
--------o----------o------
-3 -2 -1 0 1 2 3 4 5
Then we pick test points in the three regions between
or beyond those two critical point.
1. Pick a number in the region (-∞,), say -1 and
substitute it in
That is false so (-∞,) is NOT part of the domaim.
2. Pick a number in the region (,3) , say 0 and
substitute it in
That is true so (,3) is part of the domaim.
3. Pick a number in the region (3,∞), say 4 and
substitute it in
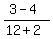
That is false so (3,∞) is NOT part of the domaim.
Now we must test the critical numbers in the
original inequality to see if they themselves
are solutions or not.
Test the endpoint in
s(x) =
s() = 
= 
= 
= Undefined
So the endpoint is NOT part of the domain.
Test the endpoint 3 in
s(x) =
s(x) = 
= s(x) = 
= 0
So the endpoint 3 is part of the domain.
So the graph of the domain is
--------o==========●------
-3 -2 -1 0 1 2 3 4 5
So the domain of s(x) is (,3]
Here's the graph of s(x). The green line is the vertical asymptote.
Edwin
