|
Question 625151: One zero of the function is i. Find the others.
f(x)=x^4-4x^3+2x^2-4x+1
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! First of all, since the degree of this polynomial is 4, there should be 4 zeros. We're given one, i. And we're looking to find the other 3.
Normally we would try to factor f(x) to find zeros. But f(x) does not factor using any of the regular factoring techniques (GCF, patterns, trinomials, grouping, rational roots). So we will have to find the zeros another way.
If a polynomial has real coefficients, like f(x) does, and if it has a complex zero, like i, then the complex conjugate of that zero will also be a zero. Since i is a zero of f(x), the complex conjugate of i will also be a zero of f(x). In general the complex conjugate of a + bi is a - bi. Our zero is i. Written in a + bi form, it would be 0 + i. The complex conjugate of 0 + i would be 0 - i (or just -i)
You may not realize it but we have just found two factors of f(x). In general, if z is a zero of a polynomial, then (x-z) is a factor of the polynomial. And we know two zeros: i and -i. So (x - i) and (x - (-i)) (or just (x + i)) are factors of f(x):
f(x) = (x - i)(x + i)(???)
To find the remaining factor(s) we could divide f(x) by the two factors. But because of the i's involved it turns out to be easier to multiply the two factors we know and then divide f(x) by the product. Multiplying (x - i)(x + i) is actually quite easy because it fits the pattern of  . So, according to the pattern: . So, according to the pattern:

Since  this simplifies: this simplifies:

Notice how the i's are gone! this is why multiplying first and then dividing makes things easier than dividing with the i's.
Next we ill divide f(x) by 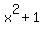 using long division: using long division:
x^2 -4x + 1
__________________________
x^2+1 / x^4 -4x^3 +2x^2 -4x +1
x^4 + x^2
-----------------
-4x^3 + x^2 -4x
-4x^3 -4x
-----------------
x^2 +1
x^2 +1
-------------
0
So  To find the last two zeros we can use the Quadratic Formula on the third factor: To find the last two zeros we can use the Quadratic Formula on the third factor:

which simplifies as follows:










So the four zeros are: i, -i, 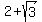 and and 
|
|
|
| |