SOLUTION: Find the average rate of change for f(x) = 3x + x from 1 and 2 and the equation of the secant line containing (1, f(1)) and (2, f(2)). I'm not understanding the secant line. Co

Algebra ->  Functions -> SOLUTION: Find the average rate of change for f(x) = 3x + x from 1 and 2 and the equation of the secant line containing (1, f(1)) and (2, f(2)). I'm not understanding the secant line. Co      Log On


   

Question 536295: Find the average rate of change for
f(x) = 3x + x from 1 and 2 and the equation of the secant line containing (1, f(1)) and (2, f(2)). I'm not understanding the secant line. Could someone please explain this to me?
Answer by fcabanski(1391) About Me  (Show Source):
You can put this solution on YOUR website!
The secant line goes through two points on a graph. Find that line by plugging in those x-values (1 and 2) into the equation. Each results is the corresponding y.


Then use those coordinates to find the slope of the secant line, which is the rate of change. Slope = 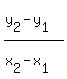%28y%5B2%5D-y%5B1%5D%29%2F%28x%5B2%5D-x%5B1%5D%29


The issue is your equation is incorrect. It's a straight line. Its secant line is itself. There has to be more to the equation, such as f(x)= 3x^2+x.

I provide online tutoring ($30/hr) and personal problem solving
($3.50-$5.50 per problem. Contact me (check the profile "website" which is
my email address.