SOLUTION: Express the length L of a chord of a circle with radius 10cm as a function of the central angle

There are two methods.  The answers look different but are
equivalent.  I'll do it both ways:


If you have studied the law of cosines then:









If you haven't studied the law of cosines, it can be done another way,
but it involves the angle 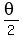 instead of .

For doing it that way, draw in this green median, which, since the triangle
is isoceles, is the bisector of the central angle as well as the 
perpendicular bisector of the chord, forming two congruent right triangles.



Looking at the upper right triangle only, we see that



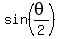
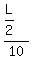Multiply both sides by 10



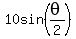
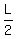Multiply both sides by 2



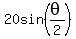
Edwin