SOLUTION: Could one of the tutors please help me with this question as I am not able to solve it myself. Any help will be greatly appreciated. A gas tank on a dock has a small puncture an

Algebra ->  Functions -> SOLUTION: Could one of the tutors please help me with this question as I am not able to solve it myself. Any help will be greatly appreciated. A gas tank on a dock has a small puncture an      Log On


   

Question 202485: Could one of the tutors please help me with this question as I am not able to solve it myself. Any help will be greatly appreciated.
A gas tank on a dock has a small puncture and is leaking gas at the rate of 1cm^3/min into a lake. It forms a circular slick that is 1mm thick on the surface of the water.(4 marks, 1 mark each)
a) Find the amount of gas leaked as a function of time.
b) State the radius of the slick as a function of its volume.
c) State the radius of the slick as a function of time.
d) What is the radius of the slick after 40 minutes?
Answer by Theo(13342) About Me  (Show Source):
You can put this solution on YOUR website!
A gas tank on a dock has a small puncture and is leaking gas at the rate of 1cm^3/min into a lake. It forms a circular slick that is 1mm thick on the surface of the water.(4 marks, 1 mark each)
-----
a) Find the amount of gas leaked as a function of time.
b) State the radius of the slick as a function of its volume.
c) State the radius of the slick as a function of time.
d) What is the radius of the slick after 40 minutes?
-----
volume of the leak = m * (1cm^3) where m represents the number of minutes.
-----
the leak forms a cylinder on the surface of the lake.
volume of a cylinder is equal to 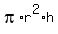pi%2Ar%5E2%2Ah
where:
r = radius of the slick
h = height of the slick.
-----
since h is expressed in mm, and v is expressed in cm^3, we need to convert h to cm.
since 1 mm = (.1)*cm, the conversion factor is (.1)*h.
the formula becomes:
v+=+pi%2Ar%5E2%2A%28.1%29%2Ah
-----
since volume of the leak = m*(1cm^3) and volume of the cylinder = pi%2Ar%5E2%2A%28.1%29%2Ah, then:
v+=+m%2Acm%5E3+=+pi%2Ar%5E2%2A%28.1%29%2Ah
-----
your first question was:
a) Find the amount of gas leaked as a function of time.
this is expressed as the formula:
v+=+m%2Acm%5E3%29
where v = volume of the leakage, and m = number of minutes.
in 1 minute, the volume is 1*cm^3.
in 40 minutes the volume is 40*cm^3.
-----
your second question was:
b) State the radius of the slick as a function of its volume.
the formula for the volume of the slick is:
v+=+pi%2Ar%5E2%2A%28.1%29%2Ah
if we divide both sides of this equation by pi%2A%28.1%29%2Ah, we get:
r%5E2+=+v%2F%28pi%2A%28.1%29%2Ah%29
if we take the square root of both sides, we get:
r+=+sqrt%28v%2F%28pi%2A%28.1%29%2Ah%29%29
that would be the function that you are looking for.
-----
your third question was:
c) State the radius of the slick as a function of time.
since the volume of the slick was expressed as a function of time as follows:
v+=+m%2Acm%5E3+=+pi%2Ar%5E2%2A%28.1%29%2Ah
we can substitute m%2Acm%5E3 for v in the equation above to express it as a function of time.
the equation would then be:
r+=+sqrt%28%28m%2Acm%5E3%29%2F%28pi%2A%28.1%29%2Ah%29%29
-----
the fourth question was:
d) What is the radius of the slick after 40 minutes?
the equation as a function of time was:
r+=+sqrt%28%28m%2Acm%5E3%29%2F%28pi%2A%28.1%29%2Ah%29%29
m = 40 so the equation becomes:
r+=+sqrt%28%2840%2Acm%5E3%29%2F%28pi%2A%28.1%29%2Ah%29%29
h = (.1)*cm so the equation becomes:
r+=+sqrt%28%2840%2Acm%5E3%29%2F%28pi%2A%28.1%2Acm%29%29%29
this becomes:
r+=+sqrt%28127.3239545%2Acm%5E2%29
which becomes:
r+=+11.28379167%2Acm%29
-----
to prove this answer is correct, let's go back and see if we can generate the volume again.
we know the volume is 40*cm^3 because the rate of leakage was 1*cm^3 per minute and it was leaking for 40 minutes.
we know that r = 11.28379167*cm
we know that h = .1*cm
we know what pi is
we know that the formula for the volume of the cylinder is:
40%2Acm%5E3+=+pi%2Ar%5E2%2Ah
we substitute known values into the equation to get:
40%2Acm%5E3+=+pi%2A%2811.28379167%2Acm%29%5E2%2A%28.1%2Acm%29
we simplify to get:
40%2Acm%5E3+=+pi%2A127.3239545%2Acm%5E2%2A.1%2Acm
which becomes:
40%2Acm%5E3+=+400%2Acm%5E2%2A%28.1%2Acm%29
which becomes:
40%2Acm%5E3+=+40%2Acm%5E3
-----
since the equation is true, we know that our calculation of the radius is correct.
if you did not translate the height of the slick from mm to cm you would have been led to the wrong answer. that part was important.
-----
you also could have left the cm^2 and the cm^3 and the cm out of the equation as they were implied.
if you said v = m instead of v = m*(1*cm^3), as long as everybody knew that m was espressed in minutes and v was expressed in cm^3, it should have been ok.
similarly with h = .1*cm which could have been stated as h = .1 under the assumption that h was expressed in cm.
similarly with r = x*cm, or r^2 = y*cm^2. the cm could have been left out without changing the equation as long as everybody knew that r was expressed in cm as well.
-----
your formulas without the cm would look like this:
v = m where m = minutes and v = number of cm^3.
v (cylinder) = pi%2Ar%5E2%2A%28.1%29%2Ah where v = number of cm^3 and r = number of cm and (.1)*h = number of cm.
you would have had:
40 = pi * r^2 * (.1) * h, which would have translated to:
40 = pi * (11.28379167)^2 * (.1) which would have yielded 40.
at the end you would then add cm^3 to state that v = 40 cm^3.
either way it should be accurate so just choose the way you prefer.
-----