SOLUTION: I need help please, I could not find an example in the book. Transform the function f(x)=x^2-10x+32 to the form f(x)=c(x-h)^2+k, where c,h,and k are constants, by completing the

Algebra ->  Functions -> SOLUTION: I need help please, I could not find an example in the book. Transform the function f(x)=x^2-10x+32 to the form f(x)=c(x-h)^2+k, where c,h,and k are constants, by completing the      Log On


   

Question 182730: I need help please, I could not find an example in the book.
Transform the function f(x)=x^2-10x+32 to the form f(x)=c(x-h)^2+k, where c,h,and k are constants, by completing the square.
Thank-you
Found 2 solutions by vleith, solver91311:
Answer by vleith(2983) About Me  (Show Source):
You can put this solution on YOUR website!
Solved by pluggable solver: COMPLETING THE SQUARE solver for quadratics
Read this lesson on completing the square by prince_abubu, if you do not know how to complete the square.
Let's convert 1x%5E2%2B-10x%2B32=0 to standard form by dividing both sides by 1:
We have: 1x%5E2%2B-10x%2B32=0. What we want to do now is to change this equation to a complete square %28x%2Bsomenumber%29%5E2+%2B+othernumber. How can we find out values of somenumber and othernumber that would make it work?
Look at %28x%2Bsomenumber%29%5E2: %28x%2Bsomenumber%29%5E2+=+x%5E2%2B2%2Asomenumber%2Ax+%2B+somenumber%5E2. Since the coefficient in our equation 1x%5E2%2Bhighlight_red%28+-10%29+%2A+x%2B32=0 that goes in front of x is -10, we know that -10=2*somenumber, or somenumber+=+-10%2F2. So, we know that our equation can be rewritten as 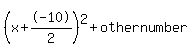%28x%2B-10%2F2%29%5E2+%2B+othernumber, and we do not yet know the other number.
We are almost there. Finding the other number is simply a matter of not making too many mistakes. We need to find 'other number' such that 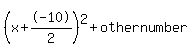%28x%2B-10%2F2%29%5E2+%2B+othernumber is equivalent to our original equation 1x%5E2%2B-10x%2Bhighlight_green%28+32+%29=0.


The highlighted red part must be equal to 32 (highlighted green part).

-10%5E2%2F4+%2B+othernumber+=+32, or othernumber+=+32--10%5E2%2F4+=+7.
So, the equation converts to %28x%2B-10%2F2%29%5E2+%2B+7+=+0, or %28x%2B-10%2F2%29%5E2+=+-7.

Our equation converted to a square 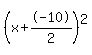%28x%2B-10%2F2%29%5E2, equated to a number (-7).

There is no number whose square can be negative. So, there is no solution to this equation

Answer by solver91311(24713) About Me  (Show Source):
You can put this solution on YOUR website!



Step 1: Divide the coefficient on the x term by 2.

Step 2: Square the result.

Step 3: Re-write the given constant term as the sum of the results of step 2 and some number. You should now have an x-squared term, an x term, and two constant terms, the first of which is the result of step 2, and the sum of the two is the original constant term.

Step 4: The first three terms are now a perfect square trinomial. Factor it. You should now have a binomial in x squared plus (or minus perhaps) a constant.

In this case c is 1, h will be the second term of the binomial, and k will be the leftover constant.



John