|
Question 162116This question is from textbook
: Solve each of the followning problems by setting up and solving an alebraic equation. One of two supplementary angles is five times as large as the other. Find the measue of each angle.
This question is from textbook
Found 2 solutions by eperette, Electrified_Levi:
Answer by eperette(173)   (Show Source): (Show Source):
Answer by Electrified_Levi(103)   (Show Source): (Show Source):
You can put this solution on YOUR website! Hi, Hope I can help,
.
Solve each of the following problems by setting up and solving an algebraic equation. One of two supplementary angles is five times as large as the other. Find the measure of each angle.
.
Supplementary angles always add up to 180 degrees, so both angles will add up to 180
.
We need to find the two angles in variable form
.
One of two supplementary angles is five times as large as the other.
.
First angle = 
.
Second angle =  , we can name the " other angle", "x" , we can name the " other angle", "x"
.
Other angle = 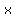 , we can replace "other angle" with , we can replace "other angle" with 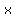 , in our two angles , in our two angles
.
First angle =  = = 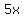
.
Second angle = 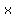
.
Since these two angles add up to 180, we can put the angles into an equation, we will add the two angles together, and they equal 180
.
First angle = 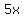
.
Second angle = 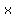
.
 , we can now solve for "x" , we can now solve for "x"
.
 = =  = =  , to find "x" divide each side by "6" , to find "x" divide each side by "6"
.
 = =  = =  = =  = = 
.
x =  , we can check by replacing "x" with "30" in the original equation , we can check by replacing "x" with "30" in the original equation
.
 = =  = =  = =  = =  ( True ) ( True )
.
x =  , we can replace "x" with "30" in our angle measurements , we can replace "x" with "30" in our angle measurements
.
First angle = 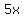 = =  = = 
.
Second angle = 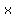 = =  = = 
.
 is 5 times the second angle is 5 times the second angle 
.
First angle =  degrees degrees
.
Second angle =  degrees degrees
.
Hope I helped, Levi
|
|
|
| |