|
Question 124610This question is from textbook
: Can you please help me with this problem a.s.a.p?
The function f(x)=((x-1)/(x-4)sqrt(x+2)) is negative for x in
a.(1,4)
b.(-infinity,4)
c.(-infinity,1)
d.(4,infinity)
I think the answer is b.,am I right? Please help as soon as possible.
This question is from textbook
Answer by bucky(2189)   (Show Source): (Show Source):
You can put this solution on YOUR website! As I understand your problem you are given:
.

.
Suppose that we replace f(x) with y, just so it is a little easier to think about this equation in
a graph format. With that replacement the equation becomes:
.

.
What the problem now means is that we need to determine for what values of x will y become
a negative real value ...
.
Let's think about this problem. There are a number of possibilities that are possible:
.
y may be real and have a positive value or
y may be real and have a negative value or
y may be real and equal to zero or
y may not have a real value
.
The thing we need to realize is that there are three critical values of x. These values are
where x causes one of the factors to become zero.
.
Why are we concerned where x causes a zero??? ... because when such a zero occurs, something
critical may be happening. The graph of y versus x may be crossing or touching the x-axis, the
graph of y versus x may exploding toward y = +infinity or toward y = - infinity, or the graph
may be transitioning to a region where it does not have a real value.
.
Let's apply that to this problem. Start with looking at the radical:
.
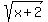
.
That is one of the factors of this problem and x + 2 reaches a critical value of zero when
.
x + 2 = 0
.
which occurs when x = -2
.
Let's see what happens to this factor when the value of x lies to the left of -2 on the x-axis.
Just as a trial, let x = -3. When that occurs, the radical becomes:
.

.
But the square root of -1 is not a real number. And if you think about it, any value of x that is
to the left of -2 on the x-axis will produce the square root of a negative number. Therefore,
we can't have a real value for y if x is to the left of -2 on the x-axis. Therefore, we
can forget about any real answer for y if the value of x is less than (to the left of) -2
on the x-axis.
.
The next critical value for x occurs when we look at x - 1. Setting x - 1 equal to zero tells
us that the next critical point occurs when
.
x - 1 = 0 which means that
.
x = +1
.
So between we need to examine the value of y between x = -2 and x = +1. We can do that by
picking some value of x in that region and solving for y. An easy value to pick in that
region is x = 0. Calculate y when x = 0 by going to:
.

.
and when you set x = 0 in that equation you get:
.

.
You don't need to deal with the numbers ... just the signs. The square root of 2 is plus, and
the -1 divided by the -4 is also plus. This tells you that y is positive in the region where
x is between -2 and +1.
.
The next critical value occurs where x - 4 is zero or:
.
x - 4 = 0 so
.
x = +4
.
What happens to y when the values of x go from +1 to +4? How about we pick a value for x
in that area ... say x = +2 and calculate the value of y for that value ...
.

.
Substitute +2 for x and this becomes:
.

.
Look at the signs of the factors ... (2-1) is positive ... (2-4) is negative ... and sqrt(2+2)
is positive. This means that y will have a negative value because a plus divided by a negative
is negative and multiplied by the positive radical is still negative.
.
Therefore, we can conclude that y (which is the value of the original function) will be negative
when x is in the interval +2 to +4.
.
No more critical values occur after x = +4. So what about when x is greater than +4? What will
be the sign of y in the interval of x above +4 all the way to + infinity? Let's just pick any
value of x in that interval and determine the sign of y in that interval. Suppose we let
x = +5. Then substitute that value into the equation for y and you have:
.

.
Notice that all 3 factors ... (5-1), (5-4), and sqrt(5+2) are positive and therefore,
y is positive. This will be true for any value of x greater than +4.
.
So the only region where y (the value of the function) is negative is the interval from
x = +1 to x < +4.
.
Note that x cannot equal +4 because if it does, the factor (x - 4) in the function becomes
zero and division by zero is not allowed in algebra.
.
This method of analysis is sort of a take-off on a process called Bode plotting, in case you
are interested in studying it further.
.
Hope this helps you with analyzing this problem and finding where you went a little astray
in coming up with the answer you did.
.
.
|
|
|
| |