|
Question 123559: I am practicing finding the domain of an expression in interval notation. A particular problem has brought confusion
radical x(square)-7x-18/x-12
I know that the denomenator cannot be zero, otherwise it would be undefined. So would the answer be [-9,2] U [2,infinity) and x cannot =12 ?
Am I on the right track with this?
Found 2 solutions by stanbon, chitra:
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! radical x(square)-7x-18/x-12
--------------------------------
Comment: It is difficult to tell what your numerator is.
Maybe it is sqrt(x^2-7x-18)
If that is true, x^2-7x-18 must not be negative
(x-9)(x+2) < 0
Draw a number line; plot the points x=-2 and x=9
Find which interval contains the solution set:
If x=-3 you get (-3-9)(-3+2)< 0 which is false
If x=0 you get (0-9)(0+2)< 0 which is true
If x= 10 you get (10-9)(10+2)< 0 which is false
-------------------------------------------
So, the domain cannot be 12 and it cannot be in the interval (-2,9)
The domain is all Real Numbers except 12 or -2 < x < 9
====================
Cheers,
Stan H.
Answer by chitra(359)  (Show Source): (Show Source):
You can put this solution on YOUR website! Can you tell me if this is the right problem?
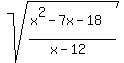
To calculate the domain for such kind of functions with radical signs we just consider the function in the denominator.
So the function in the denominator is x - 12. We now check the number which makes the denominator zero. That is 12. Hence the domain of this function would be the set of all real numbers except.
so in interval notation it would be: [-infinity, 12) U (12, infinity]
Coming to the numerator. The values that make this function zero are 9, -2
Hence, the interval notation is [infinity,-2) U (-2,9) U (9, infinity]
|
|
|
| |