SOLUTION: Fill in the blanks. If f(x) is an even function and g(x) is an even function and h(x) is an even function, then f(x) + g(x) + h(x) is an ___ function. If f(x) is an odd f

Algebra ->  Functions -> SOLUTION: Fill in the blanks. If f(x) is an even function and g(x) is an even function and h(x) is an even function, then f(x) + g(x) + h(x) is an ___ function. If f(x) is an odd f      Log On


   

Question 1209870: Fill in the blanks.

If f(x) is an even function and g(x) is an even function and h(x) is an even function, then f(x) + g(x) + h(x) is an ___ function.

If f(x) is an odd function and g(x) is an odd function and h(x) is an even function, then f(x)*g(x) + h(x) is an ___ function.

If f(x) is an even function and g(x) is an odd function and h(x) is an odd function, then f(x)*(g(x) + h(x)) is an ___ function.

If f(x) is an odd function and g(x) is an even function and h(x) is an odd function, then f(x)*g(x)*h(x) is an ___ function.
Found 4 solutions by CPhill, Edwin McCravy, ikleyn, math_tutor2020:
Answer by CPhill(1959) About Me  (Show Source):
You can put this solution on YOUR website!
Let's break down each scenario:
**Key Properties:**
* **Even Function:** f(-x) = f(x)
* **Odd Function:** f(-x) = -f(x)
**1. If f(x), g(x), and h(x) are all even functions, then f(x) + g(x) + h(x) is an ___ function.**
* Let's test:
* [f(-x) + g(-x) + h(-x)] = f(x) + g(x) + h(x)
* Therefore, f(x) + g(x) + h(x) is an **even** function.
**2. If f(x) and g(x) are odd functions and h(x) is an even function, then f(x)*g(x) + h(x) is an ___ function.**
* Let's test:
* f(-x) * g(-x) + h(-x) = (-f(x)) * (-g(x)) + h(x) = f(x) * g(x) + h(x)
* Therefore, f(x)*g(x) + h(x) is an **even** function.
**3. If f(x) is an even function and g(x) and h(x) are odd functions, then f(x)*(g(x) + h(x)) is an ___ function.**
* Let's test:
* f(-x) * (g(-x) + h(-x)) = f(x) * (-g(x) - h(x)) = -f(x) * (g(x) + h(x))
* Therefore, f(x) * (g(x) + h(x)) is an **odd** function.
**4. If f(x) and h(x) are odd functions and g(x) is an even function, then f(x)*g(x)*h(x) is an ___ function.**
* Let's test:
* f(-x) * g(-x) * h(-x) = (-f(x)) * g(x) * (-h(x)) = f(x) * g(x) * h(x)
* Now, lets test by negating all x's.
* f(-x) * g(-x) * h(-x) = (-f(x)) * g(x) * (-h(x)) = f(x) * g(x) * h(x)
* f(-x)g(-x)h(-x) = (-f(x)) * g(x) * (-h(x)) = f(x)g(x)h(x)
* f(-x)g(-x)h(-x) = (-1)f(x) * g(x) * (-1)h(x) = f(x)g(x)h(x)
* Now lets test by negating one x at a time.
* f(-x)g(x)h(x) = (-f(x))g(x)h(x) = -f(x)g(x)h(x)
* f(x)g(-x)h(x) = f(x)g(x)h(x)
* f(x)g(x)h(-x) = f(x)g(x)(-h(x)) = -f(x)g(x)h(x)
* f(-x)g(-x)h(x) = (-f(x))g(x)h(x) = -f(x)g(x)h(x)
* f(-x)g(x)h(-x) = (-f(x))g(x)(-h(x)) = f(x)g(x)h(x)
* f(x)g(-x)h(-x) = f(x)g(x)(-h(x)) = -f(x)g(x)h(x)
* f(-x)g(-x)h(-x) = (-f(x))g(x)(-h(x)) = f(x)g(x)h(x)
* The product of two odd functions is an even function, and the product of an even and an odd function is an odd function.
* so odd * even * odd = even * odd = odd.
* Therefore, f(x) * g(x) * h(x) is an **odd** function.

Answer by Edwin McCravy(20056) About Me  (Show Source):
You can put this solution on YOUR website!

An even function is symmetrical with respect to the x axis,
An odd function is symmetrical with respect to the origin.

Two examples of even functions are f(x) = x2 and g(x) = x4 
graph%28100%2C100%2C-2%2C2%2C-2%2C2%2Cx%5E2%29   graph%28100%2C100%2C-2%2C2%2C-2%2C2%2Cx%5E4%29
If you add two even functions, you get:
graph%28100%2C100%2C-2%2C2%2C-2%2C2%2Cx%5E2%2Bx%5E4%29, which is an even function. 
If you multiply two even functions, you get:
graph%28100%2C100%2C-2%2C2%2C-2%2C2%2Cx%5E2%2Ax%5E4%29, which is an even function. 

Two examples of odd functions are h(x) = x3 and k(x) = x5 
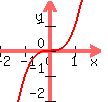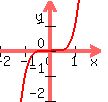graph%28100%2C100%2C-2%2C2%2C-2%2C2%2Cx%5E3%29   graph%28100%2C100%2C-2%2C2%2C-2%2C2%2Cx%5E5%29
If you add two odd functions, you get:
graph%28100%2C100%2C-2%2C2%2C-2%2C2%2Cx%5E3%2Bx%5E5%29, which is an odd function.
If you multiply two odd functions, you get:
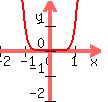graph%28100%2C100%2C-2%2C2%2C-2%2C2%2Cx%5E3%2Ax%5E5%29, which is an even function.

An example of adding an even function to an odd function is adding 
f(x) = x2 and  h(x) = x3
You get:
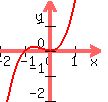graph%28100%2C100%2C-2%2C2%2C-2%2C2%2Cx%5E2%2Bx%5E3%29 <---Watch out for this case!!

If you look close, that function is nether even nor odd. It is neither
symmetrical with respect to the y axis nor the origin.

If you multiply an even function by an odd function, you get
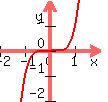graph%28100%2C100%2C-2%2C2%2C-2%2C2%2Cx%5E2%2Ax%5E3%29, which is an odd function,

Now you have all the information you need to answer the questions.

And, for godssake, don't trust Artificial Intelligence's solutions.  
Sometimes he's right and sometimes he's wrong.  He is still learning.
Someday he'll get them all right when he learns enough, but at the 
present, don't trust him!

Edwin

Answer by ikleyn(52793) About Me  (Show Source):
You can put this solution on YOUR website!
.
Fill in the blanks.

(a) If f(x) is an even function and g(x) is an even function and h(x) is an even function, then f(x) + g(x) + h(x) is an ___ function.

(b) If f(x) is an odd function and g(x) is an odd function and h(x) is an even function, then f(x)*g(x) + h(x) is an ___ function.

(c) If f(x) is an even function and g(x) is an odd function and h(x) is an odd function, then f(x)*(g(x) + h(x)) is an ___ function.

(d) If f(x) is an odd function and g(x) is an even function and h(x) is an odd function, then f(x)*g(x)*h(x) is an ___ function.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~


(a) The answer is highlight%28even%29.

(b) The answer is highlight%28even%29.

(c) The answer is highlight%28odd%29.

(d) The answer is highlight%28even%29.


The answer for (d) in the post by @CPhill is wrong.



Answer by math_tutor2020(3817) About Me  (Show Source):
You can put this solution on YOUR website!

Problem 1

If f(x) is an even function, then f(-x) = f(x) for all x in the domain.
This produces symmetry about the y axis.
Since functions g and h are even, we know that
g(-x) = g(x) and h(-x) = h(x)

Then,
k(x) = f(x)+g(x)+h(x)
k(-x) = f(-x)+g(-x)+h(-x) ....... replace each x with -x
k(-x) = f(x)+g(x)+h(x) ........ apply definitions shown above
k(-x) = k(x)
Therefore k(x) is even

You can use a graphing tool like Desmos or GeoGebra to help confirm the answer.
For instance you can form these functions
f(x) = x^2
g(x) = 10x^4-7
h(x) = 8x^6+3x^2
A polynomial is an even function when all exponents are even numbers.
Think of the -7 as -7x^0 in the g(x) function.

------------------------------------------------------------
Problem 2

If f(x) is an odd function then f(-x) = -f(x) for all x in the domain.
g(-x) = -g(x) is the case here as well since we're told g(x) is also odd.
h(-x) = h(x) since h(x) is even.

k(x) = f(x)*g(x) + h(x)
k(-x) = f(-x)*g(-x) + h(-x)
k(-x) = -1*f(x)*(-1)*g(x) + h(x)
k(-x) = (-1)*(-1)*f(x)*g(x) + h(x)
k(-x) = f(x)*g(x) + h(x)
k(-x) = k(x)
This proves that k(x) is even

------------------------------------------------------------
Problem 3

f = even function
g,h = odd functions

f(-x) = f(x)
g(-x) = -g(x)
h(-x) = -h(x)

k(x) = f(x)*( g(x)+h(x) )
k(-x) = f(-x)*( g(-x)+h(-x) )
k(-x) = f(x)*( -g(x)-h(x) )
k(-x) = f(x)*(-1)*( g(x)+h(x) )
k(-x) = -f(x)*( g(x)+h(x) )
k(-x) = -k(x)
We have shown that k(x) is odd

------------------------------------------------------------
Problem 4

f,h = odd functions
g = even

f(-x) = -f(x) and h(-x) = -h(x)
g(-x) = g(x)

k(x) = f(x)*g(x)*h(x)
k(-x) = f(-x)*g(-x)*h(-x)
k(-x) = -f(x)*g(x)*(-1)*h(x)
k(-x) = (-1)*(-1)*f(x)*g(x)*h(x)
k(-x) = f(x)*g(x)*h(x)
k(-x) = k(x)
k(x) is an even function.

------------------------------------------------------------
------------------------------------------------------------
Answers:
1. even
2. even
3. odd
4. even
In other words, answer 3 is the only "odd" while the others are "even".