SOLUTION: Determine if the function is increasing, decreasing, even, odd, and/or invertible on its natural domain: f(x) = x + 1 + 1/x I already found this function is neither even nor odd

The domain is the set of all real numbers except of x= 0.


You may plot the graphs of this function.

For it, go to web-site  www.desmos.com/calculator


Find there free of charge plotting tool for common use.

Print there the formula for this function.


You will see the plot immediately.


The plot consists of two branches. 

One branch is in the 1st quadrant, where x i greater than 0.

You will see that this function f(x) is decreasing in the interval 0 < x < 1 
and is increasing in the interval (1,oo).


The other branch is in the 3rd quarter, where x < 0.

You see there that this function is increasing in the interval (-oo,-1) and is decreasing in the interval (-1,0).


So, from the plots you have a huge amount of information.


Next, you may get the same conclusions using formal considerations.


For it, take the derivative   f'(x) = 1 -  = .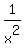


    Use the standard recipes from Calculus:

        The function is increasing where its derivative is positive.

        The function is decreasing where its derivative is negative.



Having the derivative, you can analyze the behavior of the function in each 
of these 4 intervals, and you inevitably will come to the same conclusions LOGICALLY, to which you observed VISUALLY.