|
Question 1200807: Given that y=(r^3-8)^4/5, how do I find?
a. Inverse
b. Any six (6) possible values that will be included in the domain of the above
function
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! your equation is y = (r^3 - 8) ^ (4/5)
let y = r and r = y to get:
r = (y^3 - 8) ^ (4/5)
raise both sides of this equation by the 5/4 power to get:
r^(5/4) = y^3 - 8
add 8 to both sides of the equation to get:
r^( 5/4) + 8 = y^3
raise both sides of the equation to the 1/3 power to get:
(r^(5/4) + 8) ^ (1/3) = y
that's your inverse equation.
to graph this equation, let x = r to get:
(x^(5/4) + 8) ^ (1/3) = y
the graph looks like this.
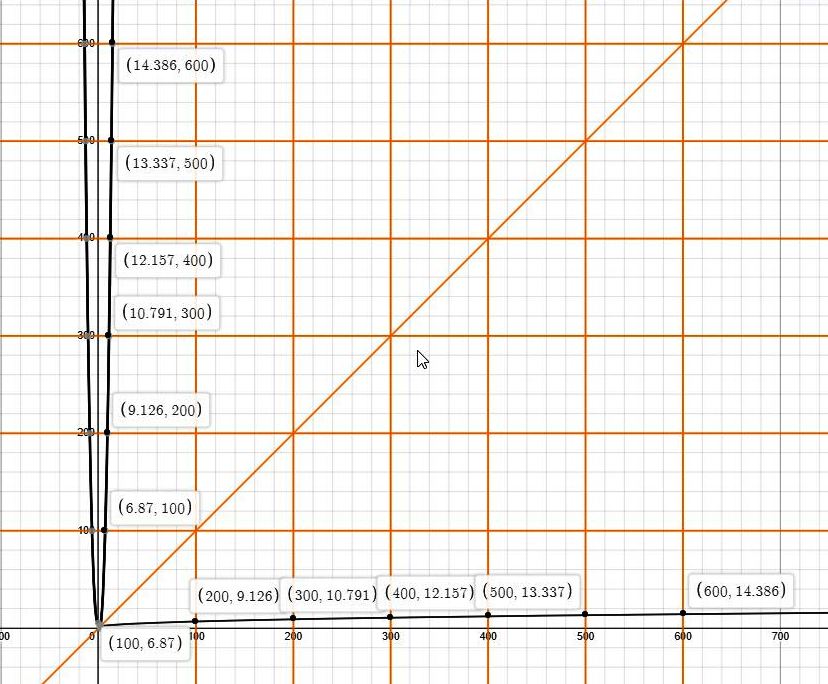
it is showing 2 equations.
the first equation is y = (x^3 - 8) ^ (4/5)
the second equation, which is the inverse euaation is y = (x^(5/4) + 8) ^ (1/3)
the only difference between the graphed equations and the original equations is the x is used in place of r.
your 6 possible values in the domain are x = 100, 200, 300, 400, 500, 600.
as you can see fromk the graph, they will generate corresponding y values where (x,y) = (y,x).
for example, the corresponding value for the point (12.157,400) in the original equation, will generate (400,12.157) in the inverse equation.
note that only the positive side of the original equation generates a corresponding inverse equation.
the negative side of the original equation will not generate an inverse because the fourth root of a number cannot be negative.
|
|
|
| |