|
Question 1200364: In a certain state the maximum speed permitted on freeways is 65 mi/h, and the minimum is 40 mi/h. The fine F for violating these limits is $25 for every mile above the maximum or below the minimum.
(a) Complete the expressions in the following piecewise defined function, where x is the speed (in mi/h) at which you are driving.
{ (blank) If 0 < x < 40
f(x) = { (blank) If 40 <_ x <_ 65
{ (blank) If x > 65
(b) Find F(25), F(45), and F(80).
F(25)=
F(45)=
F(80)=
Found 2 solutions by ikleyn, math_tutor2020:
Answer by ikleyn(52776)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
(a) If 0 < x < 40,
then the fine is calculated this way: it is the product of $25 and (40-x).
So, if 0 < x < 40, then fine F(x) = 25*(40-x) dollars.
If 40 <= x <= 65,
then there is no fine; or, you can write F(x) = 0.
So, if 40 <= x <= 65, then fine F(x) = 0 dollars.
If 65 < x,
then the fine is calculated this way: it is the product of $25 and (x-65).
Again, if 65 < x, then fine F(x) = 25*(x-65) dollars.
Now you have enough (the full instructions) to calculate everything in part (b).
Make the remained calculations for part (b) on your own.
You can report me your results.
If you do, I will check it for you at no charge.
/////////////////
If you will post me something related to this problem, then refer to the problem's ID number 1200364.
Otherwise I will not know to whom to answer.
Answer by math_tutor2020(3816)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Part (a)
x = speed in mph
If the driver obeys the law, then their speed is somewhere between 40 mph and 65 mph. This includes both endpoints.
Symbolically, if  , then the driver is obeying the law and no fines are issued (assuming no other vehicle laws are broken). , then the driver is obeying the law and no fines are issued (assuming no other vehicle laws are broken).
We would say f(x) = 0 for all x values in this interval.
This means we write "0" without quotes into the middle blank box.
If on the other hand the driver is going too slow, then they are fined $25 for every mile per hour below the speed minimum.
For instance, if they drive at 30 mph, then their fine would be 10*25 = 250 dollars.
The 10 refers to the gap from 30 to 40, ie. the driver is 10 mph under the speed limit.
To represent that gap more generally, we write 40-x where 0 < x < 40 is the case.
Then multiply that with the $25 mentioned to get 25(40-x).
You could distribute the 25 through, but I advise against it. Why? Because you lose the info about the gap from 40 to x.
We'll write "25(40-x)" into the first blank box.
The third and final blank box will get "25(x-65)" for similar reasoning as earlier.
The x-65 represents the gap from x to 65 where x > 65
Example: The driver was caught going x = 70 mph
The fine would be 25(x-65) = 25(70-65) = 25(5) = 125 dollars.
This is what the piecewise function would look like

It is another way to say the following:
- If
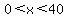 then f(x) = 25(40-x) then f(x) = 25(40-x) - If
 then f(x) = 0 then f(x) = 0 - If
 then f(x) = 25(x-65) then f(x) = 25(x-65)
====================================================
Part (b)
The first task is to compute f(25)
We want to find f(x) when the input is x = 25.
We're in the 0 < x < 40 interval, so we focus on the first piece.
f(x) = 25(40-x)
f(25) = 25(40-25)
f(25) = 25(15)
f(25) = 375
A person traveling 25 mph will be fined $375.
For the next part, f(45) = 0 because the driver is in the legal 40 mph to 65 mph interval (aka  ) )
The driver receives no fine in this case assuming no other vehicle laws are broken.
For the last part, x = 80 fits the description of x > 65
We'll focus on the last part of the piecewise function mentioned earlier.
f(x) = 25(x-65)
f(80) = 25(80-65)
f(80) = 25(15)
f(80) = 375
The fine is the same as the driver going 25 mph.
This is because the gap from 25 to 40 is the same from 65 to 80.
Both are 15 mph away from their respective endpoint.
====================================================
Summary:

F(25)= 375
F(45)= 0
F(80)= 375
|
|
|
| |