|
Question 1192587: A stone is thrown vertically upward from a 20 foot platform at a rate of 160 ft per second. The height is the stone is modeled by the quadratic function f(x)=-16t^2+160t+20
a)how long will it take for the stone to reach its maximum height?
b)what is the maximum height of the stone?
c)how long will it take for the taco to hit the ground?
Answer by ikleyn(52795)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A stone is thrown vertically upward from a 20 foot platform at a rate of 160 ft per second.
The height  of the stone is modeled by the quadratic function of the stone is modeled by the quadratic function  f(t) = -16t^2 + 160t + 20. f(t) = -16t^2 + 160t + 20.
a) how long will it take for the stone to reach its maximum height?
b) what is the maximum height of the stone?
c) how long will it take for the taco to hit the ground?
~~~~~~~~~~~~~~~~~~~~~~
The function f(t) = -16t^2 + 160t + 20 is a quadratic function, whose plot is a parabola opened down.
This quadratic function has the maximum at the value of its argument t =  , where
"a" is the coefficient at t^2 and "b" is the coefficient at t.
In your case, a= -16, b= 160, so the function gets the maximum at t = , where
"a" is the coefficient at t^2 and "b" is the coefficient at t.
In your case, a= -16, b= 160, so the function gets the maximum at t = 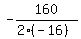 = 5 seconds.
So, the ball gets the maximum height 5 seconds after is hit straight up.
It is the ANSWER to question (a).
The maximum height is then f(5) = -16*5^2 + 120*5 + 20 = 220 feet.
It is the ANSWER to question (b).
Regarding your question (c) . . .
+-------------------------------------------------------------------+
| Question (c) asks about some tako, but I do not know |
| which tako do you mean and how does it relate to the problem. |
+-------------------------------------------------------------------+
Do you just celebrate the International FOOLs' Day,
which is scheduled on April 1 ? = 5 seconds.
So, the ball gets the maximum height 5 seconds after is hit straight up.
It is the ANSWER to question (a).
The maximum height is then f(5) = -16*5^2 + 120*5 + 20 = 220 feet.
It is the ANSWER to question (b).
Regarding your question (c) . . .
+-------------------------------------------------------------------+
| Question (c) asks about some tako, but I do not know |
| which tako do you mean and how does it relate to the problem. |
+-------------------------------------------------------------------+
Do you just celebrate the International FOOLs' Day,
which is scheduled on April 1 ?
-----------------
Solved.
----------------
To see many other similar solved problems, look into the lessons
- Problem on a projectile moving vertically up and down
- Problem on an arrow shot vertically upward
- Problem on a ball thrown vertically up from the top of a tower
- Problem on a toy rocket launched vertically up from a tall platform
in this site.
On finding the maximum/minimum of a quadratic function, learn from the lessons
- HOW TO complete the square to find the minimum/maximum of a quadratic function
- Briefly on finding the minimum/maximum of a quadratic function
- HOW TO complete the square to find the vertex of a parabola
- Briefly on finding the vertex of a parabola
in this site.
On the International FOOLs' day of April, 1 see this Wikipedia article
https://en.wikipedia.org/wiki/April_Fools%27_Day
|
|
|
| |