SOLUTION: Given the equation: f(x)= -2(x-1)^2+4, Determine the equation of its inverse. Restrict the domain of f(x) so that it’s inverse is a function. Then, state the new equation of its

Algebra ->  Functions -> SOLUTION: Given the equation: f(x)= -2(x-1)^2+4, Determine the equation of its inverse. Restrict the domain of f(x) so that it’s inverse is a function. Then, state the new equation of its       Log On


   

Question 1181302: Given the equation: f(x)= -2(x-1)^2+4, Determine the equation of its inverse. Restrict the domain of f(x) so that it’s inverse is a function. Then, state the new equation of its inverse.
Found 2 solutions by MathLover1, greenestamps:
Answer by MathLover1(20849) About Me  (Show Source):
You can put this solution on YOUR website!

Given the equation:
f%28x%29=+-2%28x-1%29%5E2%2B4
Determine the equation of its inverse.

f%28x%29=+-2%28x-1%29%5E2%2B4...replase f%28x%29 with y
y=+-2%28x-1%29%5E2%2B4.........swap variables
x=+-2%28y-1%29%5E2%2B4............solve for y
x-4=+-2%28y-1%29%5E2
%28x-4%29%2F-2=+%28y-1%29%5E2
sqrt%28%28x-4%29%2F-2%29=+y-1
y=1+%C2%B1+sqrt%28%284+-+x%29%2F2%29



domain
sqrt%28%284+-+x%29%2F2%29%3E=0
%284+-+x%29%2F2%3E=0 ....only if
%284+-+x%29%3E=0
4%3E=x
or
x%3C=4
domain is
{ x element R: x%3C=4 }
interval notation
(-infinity,4]
and your inverse is an injective (one-to-one) function







Answer by greenestamps(13195) About Me  (Show Source):
You can put this solution on YOUR website!


The given function is

y=-2%28x-1%29%5E2%2B4

This is a downward-opening parabola with vertex at (1,4). The function involves squaring an expression containing the variable; the inverse will involve taking the square root of an expression containing the variable. Since "square root" gives a positive result, the function needs to be restricted to a domain defined by (x-1) greater than or equal to 0. So the domain of the restricted function is [1,infinity).

Here is a graph of the (unrestricted) function:

graph%28400%2C400%2C-10%2C10%2C-10%2C10%2C-2%28x-1%29%5E2%2B4%29

The standard method for finding an inverse is to switch the x and y and solve for the new y.

In terms of the graph, switching the x and y means the inverse is the image of the function reflected in the line y=x.

Here is a graph of the unrestricted function (red) along with the line y=x (green):

graph%28400%2C400%2C-10%2C10%2C-10%2C10%2C-2%28x-1%29%5E2%2B4%2Cx%29

Here is the formal algebra for finding the inverse function by switching the x and y.

x+=+-2%28y-1%29%5E2%2B4
x-4+=+-2%28y-1%29%5E2
%28-1%2F2%29%28x-4%29+=+%28y-1%29%5E2
sqrt%28%28-1%2F2%29%28x-4%29%29+=+y-1
y+=+sqrt%28%28-1%2F2%29%28x-4%29%29%2B1

Here is a graph of the unrestricted function (red) and its inverse (blue), along with the line y=x (green):



You can see that the graph of the inverse function (blue) is the reflection in the line y=x (green) of the portion of the graph of the given function (red) to the right of x=1.

Now let's go back to the formal algebraic process shown above for finding the inverse by switching the x and y.

Note that that method of finding an inverse corresponds to viewing the graph of an inverse as the reflection in the line y=x of the given function.

The inverse can also be found informally, based on the concept that the inverse function "un-does" what the function does. To undo what the function does, the inverse function, compared to the given function, has to perform the opposite operations in the opposite order.

So look at the operations performed on the variable by the given function:

(1) subtract 1;
(2) square it;
(3) multiply by -2; and
(4) add 4

Therefore, the inverse function needs to...

(1) subtract 4: x-4
(2) divide by -2 (or multiply by -1/2): 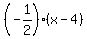%28-1%2F2%29%28x-4%29
(3) take the (positive) square root: sqrt%28%28-1%2F2%29%28x-4%29%29
(4) add 1: sqrt%28%28-1%2F2%29%28x-4%29%29%2B1

That is of course the same result we got using the formal algebra.

Furthermore, note that the steps for finding the inverse function by this informal method are EXACTLY the same as the steps used in the formal method shown above.

It is very often the case that the inverse of a relatively simple function can be found in this way much faster than with the formal algebra.