|
Question 117023: find the domain of the following:
g(t)=5^t
Answer by bucky(2189)   (Show Source): (Show Source):
You can put this solution on YOUR website! Given the function:
.

.
with the task of finding the domain of t ... the spectrum of values that t may takes.
.
When you are finding the domain of a variable, you look for values of the variable that cause a
problem in finding the value of the function. Ask yourself, "In this problem is there any value
of t that would make it impossible to find the corresponding value of g(t)?" For example,
is there a value for t that would cause a division by zero? [The answer to that question is, "No."]
Or is there a value of t that would result in the square root of a negative number? [Again,
the answer to that question is, "No."]
.
As a matter of fact, there is no real value of t that will cause any difficulty in evaluating g(t).
.
Just to convince yourself of this, you may want to try a spectrum of values for t and see
what you get for g(t). For example, try t = -10,000. That means that g(t) will be:
.

.
The denominator will be very large, meaning that g(t) will be very small. But g(t) will
be a valid real number.
.
How about when t = 0? You will get:
.

.
Any number raised to the zero power will equal +1. So when t = 0, g(t) has the valid real
value of +1.
.
Then try evaluating g(t) when t = +20,000. You will get:
.

.
The answer is that g(t) will be a very large real number, but it can be calculated.
.
This is just a little thought process to help you visualize what values t might assume ... that
is to say, "What is the domain of t?"
.
By now you should be pretty convinced that t can have any real value in the spectrum of
numbers on the number line all the way from minus infinity (-oo) to plus infinity (+oo).
.
In inequality form we can write this as:
.
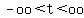
.
Hope this helps you to understand the problem a little more.
.
|
|
|
| |